ncert solutions for class 9 maths chapter 6 in Hindi

lines and angles class 9 ncert solutions समाधान अध्याय 6 रेखाएं और कोण पूर्व 6.1 कक्षा 9 गणित के लिए एनसीईआरटी समाधान का हिस्सा हैं। यहां हमने ncert solutions for class 9 maths chapter 6  दिया है।

ncert solutions for class 9 maths chapter 6 exercise 6.1

आकृति में, रेखाएँ AB और CD 0 पर प्रतिच्छेद करती हैं। यदि AOC + BOE = 70° और ∠BOD = 40°, तो BOE और प्रतिवर्त COE ज्ञात कीजिए।

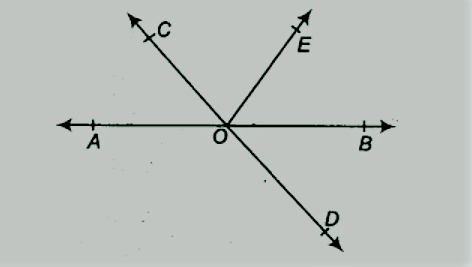ncert solutions for class 9 maths chapter 6 exercise 6.1

समाधान:

चूँकि AB एक सीधी रेखा है,

AOC + COE + ∠EOB = 180°

या (∠AOC + BOE) + ∠COE = 180° या 70° + ∠COE = 180° [ AOC + BOE = 70° (दिया है)]

या COE = 180° - 70° = 110°

प्रतिवर्त ∠COE = 360° - 110° = 250°

साथ ही, AB और CD, O पर प्रतिच्छेद करते हैं।

COA = BOD [ऊर्ध्वाधर सम्मुख कोण]

लेकिन ∠BOD = 40° [दिया है]

COA = 40°

साथ ही, ∠AOC + ∠BOE = 70°

40° + ∠BOE = 70° या ∠BOE = 70° -40° = 30°

अत: BOE = 30° और प्रतिवर्त COE = 250°।

Ex 6.1 कक्षा 9 गणित प्रश्न 2.

आकृति में, रेखाएँ XY और MN 0 पर प्रतिच्छेद करती हैं। यदि POY = 90° और a: b = 2: 3 है तो c ज्ञात कीजिए।

ncert solutions for class 9 maths chapter 6 exercise 6.1 q.2

समाधान:

चूँकि XOY एक सीधी रेखा है।

बी+ए+∠पीओवाई= 180°

लेकिन POY = 90° [दिया है]

b + a = 180° – 90° = 90° …(i)

साथ ही a : b = 2: 3 ⇒ b = 3a2 …(ii)

अब (i) और (ii) से, हम प्राप्त करते हैं

3a2 + A = 90°

⇒ 5a2 = 90°

⇒ ए = 90∘5×2=36∘ = 36°

(ii) से हमें प्राप्त होता है

बी = 32 x 36° = 54°

चूँकि XY और MN, O पर प्रतिच्छेद करते हैं,

∴ c = [a + POY] [ऊर्ध्वाधर सम्मुख कोण]

या सी = 36° + 90° = 126°

अत: c का अभीष्ट माप = 126° है।

Ex 6.1 कक्षा 9 गणित प्रश्न 3.

आकृति में, PQR = PRQ, तो सिद्ध कीजिए कि PQS = PRT।

ncert solutions for class 9 maths

समाधान:

एसटी एक सीधी रेखा है।

PQR + ∠PQS = 180° …(1) [रैखिक युग्म]

इसी प्रकार, ∠PRT + PRQ = 180° …(2) [रैखिक युग्म]

(1) और (2) से, हमारे पास है

PQS + ∠PQR = ∠PRT + PRQ

परंतु ∠PQR = PRQ [दिया है]

PQS = PRT

ncert solutions for class 9 maths chapter 6 exercise 6.1 q.4

आकृति में, यदि x + y = w + , तो सिद्ध कीजिए कि AOB एक रेखा है।

ncert solutions for class 9 maths chapter 6 exercise 6.1 q.4

समाधान:

एक बिंदु पर सभी कोणों का योग = 360°

x + y + ⇒ + w = ​​360° या, (x + y) + (⇒ + w) = 360°

लेकिन (x + y) = (⇒ + w) [दिया गया]

(x + y) + (x + y) = 360° या,

2(x + y) = 360°

या, (x + y) = 360∘2 = 180°

AOB एक सीधी रेखा है।

Ex 6.1 Class 9 Maths Question 5.

आकृति में, POQ एक रेखा है। किरण OR रेखा PQ पर लंबवत है। OS एक अन्य किरण है जो OP और OR किरणों के बीच स्थित है। साबित करो

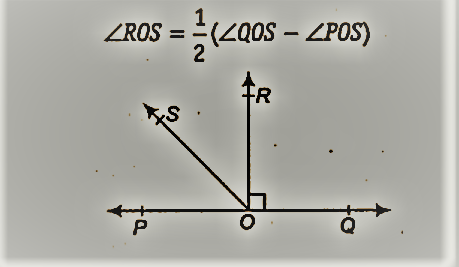lines and angles class 9 ncert solutions

समाधान:

रारा POQ एक सीधी रेखा है। [दिया गया]

POS + ROS + ROQ = 180°

लेकिन OR PQ

ROQ = 90°

POS + ∠ROS + 90° = 180°

POS + ∠ROS = 90°

ROS = 90° – POS… (1)

अब, हमारे पास ∠ROS + ROQ = QOS . है

ROS + 90° = QOS

ROS = ∠QOS - 90° ……(2)

(1) और (2) को जोड़ने पर, हमारे पास है

2 ROS = (∠QOS - POS)

ROS = 12(∠QOS−∠POS)

Ex 6.1 कक्षा 9 गणित प्रश्न 6.

यह दिया गया है कि XYZ = 64° और XY को बिंदु P तक बढ़ाया जाता है। दी गई जानकारी से एक आकृति बनाएं। यदि किरण YQ ∠ZYP को समद्विभाजित करती है, तो XYQ और प्रतिवर्त QYP ज्ञात कीजिए।

समाधान:

XYP एक सीधी रेखा है।

NCERT Solutions for Class 9 Maths Chapter 6 रेखाएँ और कोण Ex 6.1 Q6

XYZ + ZYQ + ∠QYP = 180°

64° + ZYQ + ∠QYP = 180°

[∵ XYZ = 64° (दिया गया)]

⇒ 64° + 2∠QYP = 180°

[YQ ZYP को समद्विभाजित करता है, इसलिए QYP = ZYQ]

⇒ 2∠QYP = 180° - 64° = 116°

∠QYP = 116∘2 = 58°

प्रतिवर्त QYP = 360° - 58° = 302°

तब से ∠XYQ = ∠XYZ + ∠ZYQ

⇒ ∠XYQ = 64° + ∠QYP [∵∠XYZ = 64°(Given) and ∠ZYQ = ∠QYP]
⇒ ∠XYQ = 64° + 58° = 122° [∠QYP = 58°]

अत: XYQ = 122° और प्रतिवर्त ∠QYP = 302°।

ncert solutions for class 9 maths chapter 6 exercise 6.2

Ex 6.2 Class 9 Maths Question 1.

आकृति में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || सीडी.

ncert solutions for class 9 maths chapter 6 exercise 6.2

समाधान:

आकृति में, हमारे पास CD और PQ हैं जो F पर प्रतिच्छेद करते हैं।

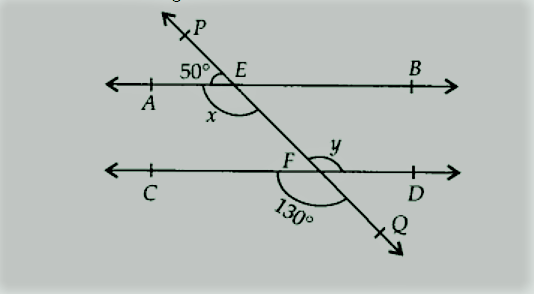ncert solutions for class 9 maths chapter 6

y = 130° …(1)

[ऊर्ध्वाधर विपरीत कोण]

फिर से, PQ एक सीधी रेखा है और EA इस पर खड़ा है।

AEP + AEQ = 180° [रैखिक जोड़ी]

या 50° + x = 180°

⇒ x = 180° – 50° = 130° …(2)

(1) और (2) से, x = y

चूंकि वे एकांतर आंतरिक कोणों के युग्म हैं।

∴ AB || CD

प्रश्न 2.

आकृति में, यदि AB || CD, CD || EF और y: z = 3: 7, x ज्ञात कीजिए।

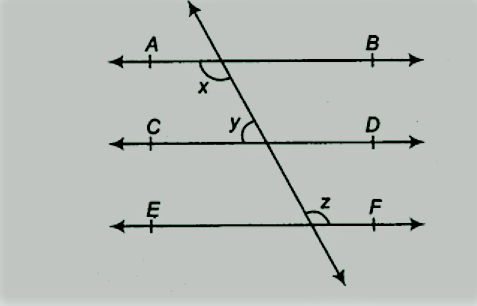lines and angles class 9 ncert solutions

समाधान:

एबी || सीडी, और सीडी || ईएफ [दिया गया]

∴ एबी || एफई

∴ x = z [वैकल्पिक आंतरिक कोण] ….(1)

फिर से, एबी || सीडी

⇒ x + y = 180° [सह-आंतरिक कोण]

⇒ z + y = 180° … (2) [द्वारा (1)]

लेकिन y : z = 3 : 7

z = 73 y = 73(180°- z) [द्वारा (2)]

10z = 7 x 180°

z = 7 x 180° /10 = 126°

(1) और (3) से, हमारे पास है

एक्स = 126 डिग्री।

Ex 6.2 कक्षा 9 गणित प्रश्न 3.

आकृति में, यदि AB || CD, EF CD और GED = 126°, AGE, ∠GEF और FGE ज्ञात कीजिए।

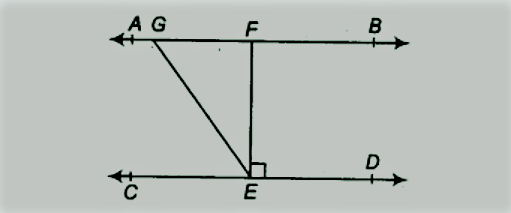ncert solutions for class 9 maths chapter 6 Q.3

समाधान:

एबी || सीडी और जीई एक तिर्यक रेखा है।

AGE = GED [वैकल्पिक आंतरिक कोण]

परंतु GED = 126° [दिया गया है]

AGE = 126°

साथ ही, GEF + ∠FED = GED

या GEF + 90° = 126° [∵ EF CD (दिया गया)]

x = z [वैकल्पिक आंतरिक कोण]… (1) फिर से, AB || सीडी

⇒ x + y = 180° [सह-आंतरिक कोण]

जीईएफ = 126° -90° = 36°

अब, एबी || सीडी और जीई एक तिर्यक रेखा है।

FGE + ∠GED = 180° [सह-आंतरिक कोण]

या FGE + 126° = 180°

या FGE = 180° – 126° = 54°

अत: AGE = 126°, ∠GEF=36° और ∠FGE = 54°।

Ex 6.2 कक्षा 9 गणित प्रश्न 4.

आकृति में, यदि PQ || ST, PQR = 110° और ∠ RST = 130°, QRS ज्ञात कीजिए।

lines and angles class 9 pdf

समाधान:

R से होकर ST के समांतर एक रेखा EF खींचिए।

ncert solutions for class 9 maths chapter 6 q.4

चूंकि  PQ || ST [Given]

और ईएफ || एसटी [निर्माण]

∴ पीक्यू || EF और QR एक तिर्यक रेखा है

∠PQR = ∠QRF [वैकल्पिक आंतरिक कोण] लेकिन ∠PQR = 110° [दिया गया है]

∴∠QRF = ∠QRS + ∠SRF = 110° …(1)

फिर से एसटी || EF और RS एक तिर्यक रेखा है

∴ ∠RST + ∠SRF = 180°  [सह-आंतरिक कोण] या 130° + ∠SRF = 180°

∠SRF  = 180° – 130° = 50°

अब, (1) से, हमें QRS + 50° = 110° . प्राप्त होता है

∠QRS = 110° - 50° = 60°

अत:∠QRS = 60°।

प्रश्न 5.

आकृति में, यदि AB || सीडी, ∠APQ = 50° और ∠PRD = 127°, x और y ज्ञात कीजिए।

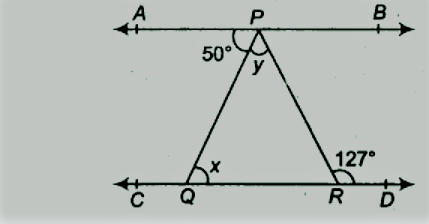ncert solutions for class 9 maths chapter 6

समाधान:

हमारे पास एबी है || सीडी और पीक्यू एक तिर्यक रेखा है।

∴ ∠APQ = ∠PQR

[वैकल्पिक आंतरिक कोण]

⇒ 50° = x [  ∠APQ  = 50° (दिया गया)]

फिर से, AB || CD और पीआर एक तिर्यक रेखा है।

 ∠APR = ∠PRD [वैकल्पिक आंतरिक कोण]

 ∠APR = 127° [ PRD = 127° (दिया गया)]

 ∠APR + ∠QPR = 127°

50° + y = 127° [ APQ = 50° (दिया गया)]

y = 127°- 50° = 77°

अत: x = 50° और y = 77°।

प्रश्न 6.

आकृति में, PQ और RS एक दूसरे के समानांतर रखे गए दो दर्पण हैं। एक आपतित किरण AB, दर्पण PQ से B पर टकराती है, परावर्तित किरण पथ BC पर चलती है और दर्पण RS से C पर टकराती है और पुनः CD के अनुदिश परावर्तित होती है। सिद्ध कीजिए कि AB || CD .

lines and angles class 9 ncert solutions

समाधान:

किरण BL ⊥PQ and CM ⊥ RS . खींचिए

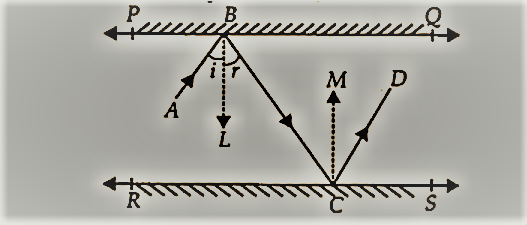ncert solutions for class 9 maths chapter 6

∵ PQ || RS ⇒ BL || CM

[∵  BL || PQ और CM || RS]

अब, बीएल || CM और BC एक तिर्यक रेखा है।

∠LBC = ∠MCB …(1) [वैकल्पिक आंतरिक कोण]

चूँकि, आपतन कोण = परावर्तन कोण

∠ABL = ∠LBC और ∠MCB = ∠MCD

∠ABL = ∠MCD …(2) [द्वारा (1)]

(1) और (2) को जोड़ने पर, हमें प्राप्त होता है

∠LBC + ∠ABL = ∠MCB + ∠MCD

 ∠ABC = ∠BCD

मैं। e., एकांतर अंत:कोणों का एक युग्म बराबर होता है।

∴ AB || CD.

ncert solutions for class 9 maths chapter 6 exercise 6.3

प्रश्न 1.

आकृति में, PQR की भुजाएँ QP और RQ क्रमशः बिंदुओं S और T तक बढ़ाई गई हैं। यदि SPR = 135° और ∠PQT = 110°, तो PRQ ज्ञात कीजिए।

ncert solutions for class 9 maths chapter 6

समाधान:

∠TQP + ∠PQR = 180°

[रैखिक जोड़ी]

⇒ 110° + ∠PQR = 180°

 ∠PQR = 180° – 110° = 70°

चूँकि PQR की भुजा QP को S तक बढ़ाया जाता है।

 ∠PQR + ∠PRQ = 135°

[एक त्रिभुज का बाह्य कोण गुण]

⇒ 70° + ∠PRQ = 135° [∠PQR = 70°]

⇒ ∠PRQ = 135° – 70° ⇒ ∠PRQ = 65°

Ex 6.3 कक्षा 9 गणित प्रश्न 2.

आकृति में, X = 62°, ∠XYZ = 54, यदि YO और ZO, ∠XYZ के क्रमशः ∠XYZ और ∠XZY के समद्विभाजक हैं, तो ∠OZY और ∠YOZ ज्ञात कीजिए।

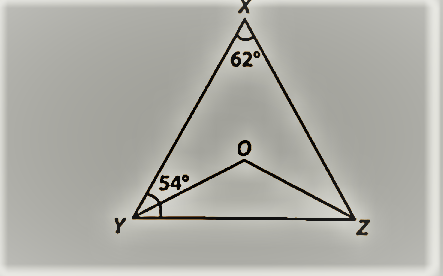ncert solutions for class 9 maths chapter 7 in hindi medium

समाधान:

∠XYZ में, हमारे पास ∠XYZ + ∠YZX + ∠ZXY = 180° . है

[एक त्रिभुज के कोणों का योग गुण]

लेकिन ∠XYZ = 54° और ∠ZXY = 62°

∴ 54° + ∠YZX + 62° = 180°

∠YZX = 180° - 54° - 62° = 64°

YO और ZO क्रमशः ∠XYZ और ∠XZY  के समद्विभाजक हैं।

∠OZY  = 12∠XYZ = 12(54°) = 27°

और OZY = 12∠YZX = 12(64°) = 32°

अब, OYZ में, हमारे पास है

∠YOZ + ∠OYZ + ∠OZY = 180°

[एक त्रिभुज के कोणों का योग गुण]

⇒ ∠YOZ + 27° + 32° = 180°

⇒ ∠YOZ = 180° -27° – 32° = 121°

अत: ∠OZY = 32° और ∠YOZ = 121°

Ex 6.3 कक्षा 9 गणित प्रश्न 3.

आकृति में, यदि AB || DE, ∠BAC = 35° और ∠CDE = 539, ∠DCE ज्ञात कीजिए।

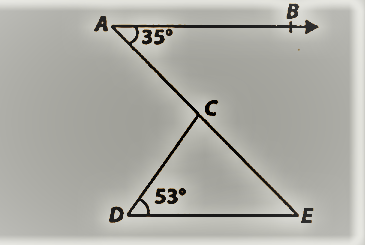ncert solutions for class 9 maths chapter 6

समाधान:

AB || DE  और AE एक तिर्यक रेखा है।

अत: ∠BAC = ∠AED

[वैकल्पिक आंतरिक कोण]

और ∠BAC = 35° [दिया है]

∴ ∠AED = 35°

अब, ∆CDE, में, हमारे पास ∠CDE + ∠DEC + ∠DCE = 180° . है

{एक त्रिभुज के कोणों का योग गुण]

∴ 53° + 35° + ∠DCE =180°

[∵ ∠DEC = ∠AED = 35° और ∠CDE = 53° (दिया गया)]

∠DCE = 180° - 53° - 35° = 92°

अत: ∠DCE = 92°

 Question 4.

आकृति में, यदि रेखाएँ PQ और RS बिंदु T पर इस प्रकार प्रतिच्छेद करती हैं कि PRT = 40°, RPT = 95° और ∠TSQ = 75°, तो SQT ज्ञात कीजिए।

lines and angles class 9 ncert solutions

समाधान:

∆PRT में, ∠P + ∠R + ∠PTR = 180°

[एक त्रिभुज के कोणों का योग गुण]

⇒ 95° + 40° + ∠PTR =180°

[ P = 95°, ∠R = 40° (दिया गया)]

∠PTR = 180° – 95° – 40° = 45°

लेकिन PQ और RS, T पर प्रतिच्छेद करते हैं।

∴ ∠PTR = ∠QTS

[ऊर्ध्वाधर विपरीत कोण]

∴ ∠QTS = 45° [ ∵ ∠PTR = 45°]

अब, TQS में, हमारे पास∠TSQ + ∠STQ + ∠SQT = 180° है।

[एक त्रिभुज के कोणों का योग गुण]

75° + 45° + ∠SQT = 180° [  ∠TSQ = 75° और ∠STQ = 45°]

∠SQT= 180° – 75° – 45° = 60°

अत: ∠SQT = 60°

प्रश्न 5.

आकृति में, यदि PQ PS, PQ||SR, ∠SQR = 2S° और ∠QRT = 65° है, तो x और y के मान ज्ञात कीजिए।

ncert solutions for class 9 maths chapter 6

समाधान:

QRS में, भुजा SR को T तक बढ़ाया जाता है।

∴ ∠QRT = ∠RQS + ∠RSQ

[एक त्रिभुज का बाह्य कोण गुण]

लेकिन ∠RQS = 28° और ∠QRT = 65°

अत: 28° + ∠RSQ = 65°

∠RSQ = 65° - 28° = 37°

चूंकि, पीक्यू || SR और QS एक तिर्यक रेखा है।

∠PQS = ∠RSQ = 37°

[वैकल्पिक आंतरिक कोण]

एक्स = 37°

पुन:,  PQ ⊥ PS ⇒ AP = 90°

अब, ∆PQS में,

∠P + ∠PQS + ∠PSQ = 180°

[एक त्रिभुज के कोणों का योग गुण]

90° + 37° + y = 180°

y = 180° - 90° - 37° = 53°

अत: x = 37° और y = 53°

ncert solutions class 9 maths :- प्रश्न 6.

आकृति में, PQR की भुजा QR को एक बिंदु S तक बढ़ाया जाता है। यदि PQR और PRS के समद्विभाजक बिंदु T पर मिलते हैं, तो सिद्ध कीजिए कि

ncert solutions for class 9 maths chapter 6

समाधान:

∆PQR में, भुजा QR को S तक बढ़ाया जाता है, इसलिए बाह्य कोण गुण से,

∠PRS = ∠P + ∠PQR

12∠PRS = 1/2∠P + 1/2∠PQR

∠TRS = 1/2∠P + ∠TQR …(1)

[∵ QT और RT क्रमशः PQR और PRS के समद्विभाजक हैं।]

अब, ∆QRT में, हमारे पास है

∠TRS = ∠TQR + ∠T …(2)

[एक त्रिभुज का बाह्य कोण गुण]

(1) और (2) से,

हमारे पास ∠TQR + 12∠P = ∠TQR + ∠T . है

1/2∠P = ∠T

1/2∠QPR = ∠QTR या ∠QTR = 1/2∠QPR