ncert solutions for class 9 maths chapter 5 in Hindi
introduction to euclid's geometry class 9 notes
निम्नलिखित में से कौन से कथन सत्य हैं और कौन से असत्य? अपने उत्तरों के लिए कारण दीजिए।
(i) एक बिंदु से केवल एक रेखा गुजर सकती है।
(ii) अनंत संख्या में रेखाएँ हैं जो दो भिन्न बिंदुओं से होकर गुजरती हैं।
(iii) एक समाप्त रेखा दोनों ओर अनिश्चित काल तक उत्पन्न की जा सकती है।
(iv) यदि दो वृत्त बराबर हों, तो उनकी त्रिज्याएँ बराबर होती हैं।
(v) आकृति में, यदि AB - PQ और PQ = XY, तो AB = XY।
Euclid Geometry class 9 solution
समाधान:
(i) असत्य
कारण: यदि हम एक कागज़ की सतह पर एक बिंदु O अंकित करते हैं। पेंसिल और स्केल का उपयोग करके, हम अनंत संख्या में सीधी रेखाएँ खींच सकते हैं
O के माध्यम से
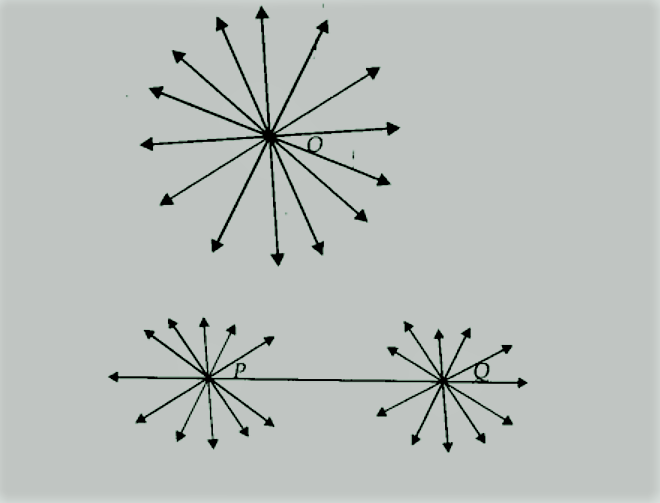
(ii) असत्य
कारण: निम्नलिखित आकृति में, P से होकर जाने वाली कई सीधी रेखाएँ हैं। Q से गुजरने वाली कई रेखाएँ हैं। लेकिन एक और केवल एक रेखा है जो P के साथ-साथ Q से भी गुजर रही है।
(iii) सच
कारण: अभिधारणा 2 कहता है कि "एक समाप्त रेखा को अनिश्चित काल तक बनाया जा सकता है।"
(iv) सत्य
कारण: एक वृत्त के क्षेत्र को दूसरे पर आरोपित करते हुए, हम उन्हें संपाती पाते हैं। तो, उनके केंद्र और सीमाएं मेल खाती हैं।
इस प्रकार, उनकी त्रिज्याएँ संपाती या बराबर होंगी।
(v) सत्य
कारण : यूक्लिड के अभिगृहीत के अनुसार जो वस्तुएँ एक ही वस्तु के बराबर होती हैं वे एक दूसरे के बराबर होती हैं।
Ex 5.1 कक्षा 9 गणित प्रश्न 2.
निम्नलिखित में से प्रत्येक पद की परिभाषा दीजिए। क्या ऐसे अन्य शब्द हैं जिन्हें पहले परिभाषित करने की आवश्यकता है? वे क्या हैं और आप उन्हें कैसे परिभाषित कर सकते हैं?
(i) समानांतर रेखाएं
(ii) लंबवत रेखाएं
(iii) रेखा खंड
(iv) एक वृत्त की त्रिज्या
(v) स्क्वायर
समाधान:
हाँ, हमें आवश्यक पदों को परिभाषित करने से पहले बिंदु, रेखा, किरण, कोण, तल, वृत्त और चतुर्भुज आदि जैसे पदों के बारे में विचार करने की आवश्यकता है।
आवश्यक शर्तों की परिभाषा नीचे दी गई है:
(i) समानांतर रेखाएँ:
एक समतल में दो रेखाएँ l और m समानांतर कहलाती हैं, यदि उनका कोई उभयनिष्ठ बिंदु नहीं है और हम उन्हें l के रूप में लिखते हैं m।introduction to euclid's geometry class 9 notes
(ii) लंबवत रेखाएँ:
एक ही तल में पड़ी दो रेखाएँ p और q लंबवत कहलाती हैं यदि वे एक समकोण बनाती हैं और हम उन्हें p ⊥ qके रूप में लिखते हैं।
(iii) रेखा खंड:
एक रेखाखंड रेखा का एक भाग होता है और इसकी एक निश्चित लंबाई होती है। इसके दो अंत बिंदु हैं। आकृति में, एक रेखा खंड को अंतिम बिंदु A और B के साथ दिखाया गया है। इसे
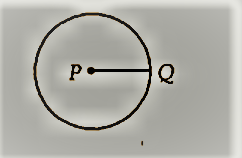
(iv) एक वृत्त की त्रिज्या:
केंद्र से वृत्त पर एक बिंदु तक की दूरी को वृत्त की त्रिज्या कहा जाता है। आकृति में, P केंद्र है और Q वृत्त पर एक बिंदु है, तो PQ त्रिज्या है।
class 9 maths chapter 5 solutions pdf
(v) वर्ग :
एक चतुर्भुज जिसमें चारों कोण समकोण हों और चारों भुजाएँ समान हों, वर्ग कहलाता है। दी गई आकृति में, PQRS एक वर्ग है।
introduction to euclid's geometry class 9 notes
euclid geometry class 9 pdf
नीचे दिए गए दो अभिधारणाओं पर विचार करें
(i) किन्हीं दो अलग-अलग बिंदुओं A और B को देखते हुए, एक तीसरा बिंदु C मौजूद है जो A और B के बीच में है।
(ii) ऐसे कम से कम तीन बिंदु मौजूद हैं जो एक ही रेखा पर नहीं हैं।
क्या इन अभिधारणाओं में कोई अपरिभाषित पद हैं? क्या ये अभिधारणा सुसंगत हैं? क्या वे यूक्लिड की अभिधारणाओं का अनुसरण करते हैं? समझाना।
समाधान:
हाँ, इन अभिधारणाओं में 'बिंदु और रेखा' जैसे अपरिभाषित पद हैं। साथ ही, ये अभिधारणाएँ सुसंगत हैं क्योंकि वे दो भिन्न स्थितियों से निपटती हैं:
(i) कहता है कि दो बिंदु A और B दिए जाने पर, उनके बीच की रेखा पर एक बिंदु C स्थित है। जबकि
(ii) कहता है कि दिए गए बिंदु A और B, आप बिंदु C को ले सकते हैं जो A और B से होकर जाने वाली रेखा पर नहीं है।
नहीं, ये अभिधारणाएँ यूक्लिड की अभिधारणाओं का अनुसरण नहीं करती हैं, हालाँकि वे अभिगृहीत से अनुसरण करती हैं, "दो अलग-अलग बिंदुओं को देखते हुए, एक अनूठी रेखा है जो उनसे होकर गुजरती है।"
ncert class 9 maths solutions : प्रश्न 4।
यदि एक बिंदु C दो बिंदुओं A और B के बीच इस प्रकार स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC = 12 AB, चित्र बनाकर समझाइए।
समाधान:
हमारे पास है,
एसी = बीसी [दिया गया]
∴ AC + AC = BC + AC
[यदि बराबर को बराबर में जोड़ा जाए तो पूर्ण बराबर होते हैं]
या 2AC = AB [∵ AC + BC = AB]
या एसी = (1/2)AB
Ex 5.1 कक्षा 9 गणित प्रश्न 5।
प्रश्न 4 में, बिंदु C को रेखाखंड AB का मध्य-बिंदु कहा जाता है। सिद्ध कीजिए कि प्रत्येक रेखाखंड में एक और केवल एक मध्य-बिंदु होता है।
समाधान:
माना दी गई रेखा AB के दो मध्य बिंदु 'C' और 'D' हैं।
एसी = (1/2)AB ……(i)
और AD = (1/2)AB ……(ii)
(i) को (ii) से घटाने पर हमें प्राप्त होता है
एडी - एसी = (1/2)AB-(1/2)AB
या AD – AC = 0 or CD = 0
∴ सी और डी मेल खाते हैं।
इस प्रकार, प्रत्येक रेखाखंड में एक और केवल एक मध्य-बिंदु होता है।
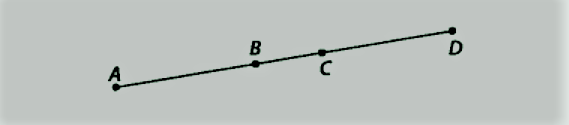
Ex 5.1 कक्षा 9 गणित प्रश्न 6.
आकृति में, यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।
ncert solutions for class 9 maths chapter 5
समाधान:
दिया गया है: एसी = बीडी
⇒ AB + BC = BC + CD
दोनों पक्षों से BC घटाने पर, हम प्राप्त करते हैं
AB + BC – BC = BC + CD – BC
[जब बराबर को बराबर में से घटाया जाता है, तो शेषफल बराबर होता है]
⇒ AB = CD
प्रश्न 7.
यूक्लिड के अभिगृहीतों की सूची में अभिगृहीत 5 को 'सार्वभौमिक सत्य' क्यों माना जाता है? (ध्यान दें कि, प्रश्न पांचवीं अभिधारणा के बारे में नहीं है।)
समाधान:
जैसा कि सभी स्थितियों में कथन सत्य है। इसलिए, इसे 'सार्वभौमिक सत्य' माना जाता है।






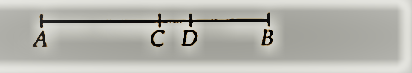








No comments:
Post a Comment