understanding quadrilaterals class 8 Notes In Hindi - class 8 math solution

Understanding Quadrilaterals Class 8 Notes - Chapter 3

 Quadrilaterals

चतुर्भुज एक प्रकार का बहुभुज है जिसमें दो विकर्णों के साथ चार भुजाएँ और चार शीर्ष और चार कोण होते हैं। चतुर्भुज विभिन्न प्रकार के होते हैं।

 

Types of Quadrilaterals

चतुर्भुजों का वर्गीकरण एक चतुर्भुज की भुजाओं या कोणों की प्रकृति पर निर्भर करता है और वे इस प्रकार हैं:

•      समलंब
•      पतंग
•      चतुर्भुज
•      वर्ग
•      आयत
•      विषमकोण

class 8 math chapter 3 : Trapezium

समलम्ब चतुर्भुज एक चतुर्भुज है जिसमें समानांतर पक्षों की एक जोड़ी होती है।

Trapezium

class 8 math chapter 3 : Parallelogram

समांतर चतुर्भुज एक चतुर्भुज होता है जिसकी सम्मुख भुजाएँ समानांतर और बराबर होती हैं।

Parallelogram

class 8 maths chapter 3 notes : Rhombus

•     समचतुर्भुज एक चतुर्भुज है जिसकी भुजाएँ समान लंबाई की होती हैं।
•     चूँकि समचतुर्भुज की सम्मुख भुजाओं की लंबाई समान होती है, इसलिए यह एक समांतर चतुर्भुज भी है।
•     एक समचतुर्भुज के विकर्ण एक दूसरे के लंब समद्विभाजक होते हैं।

   

class 8 maths chapter 3 notes : Rhombus

understanding quadrilaterals class 8 : Introduction to Curves

एक वक्र एक ज्यामितीय आकृति है, जब कागज से पेंसिल को उठाए बिना और किसी हिस्से को वापस लिए बिना कई बिंदुओं को जोड़ दिया जाता है। यह मूल रूप से एक रेखा है जिसका सीधा होना आवश्यक नहीं है।

विभिन्न प्रकार के वक्र हैं:

•     खुला वक्र: एक खुला वक्र एक ऐसा वक्र होता है जिसमें उसके किसी भी बिंदु से एक ही बिंदु तक कोई रास्ता नहीं होता है।
•     बंद वक्र: एक बंद वक्र एक वक्र है जो अपने किसी भी बिंदु से एक ही बिंदु तक पथ बनाता है।

एक वक्र हो सकता है:

   

Introduction to Curves

ncert solutions for class 8 maths chapter 3 pdf : Polygons

केवल रेखाखंडों से बना एक साधारण बंद वक्र बहुभुज कहलाता है।
बहुभुज के विभिन्न उदाहरण वर्ग, आयत, पेंटागन आदि हैं।
ध्यान दें:
एक बहुभुज की भुजाएँ एक दूसरे को काटती नहीं हैं।
उदाहरण के लिए, नीचे दी गई आकृति बहुभुज नहीं है क्योंकि इसकी भुजाएँ एक दूसरे को काटती हैं।

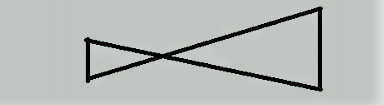Polygons

Classification of Polygons on the Basis of Number of Sides / Vertices

बहुभुजों को उनकी भुजाओं की संख्या के अनुसार वर्गीकृत किया जाता है। निम्नलिखित विभिन्न प्रकार के बहुभुजों को उनके पक्षों की संख्या के आधार पर सूचीबद्ध करता है:

•     जब तीन भुजाएँ हों, तो वह त्रिभुज होता है
•     जब चार भुजाएँ हों, तो वह चतुर्भुज होती है
•     जब पाँच भुजाएँ हों, तो वह पंचभुज है
•     जब छह भुजाएँ हों, तो वह षट्भुज होता है
•     जब सात भुजाएँ हों, तो वह सप्तभुज होता है
•     जब आठ भुजाएँ हों, तो वह अष्टभुज होती है
•     जब नौ भुजाएँ हों, तो यह अभुज है
•     जब दस भुजाएँ हों, तो वह दशभुज होती है

understanding quadrilaterals class 8 notes : Diagonals

एक विकर्ण एक बहुभुज के दो गैर-लगातार शीर्षों को जोड़ने वाला एक रेखा खंड है।

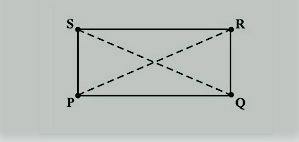Diagonals

उपरोक्त आकृति में, PR और QS विकर्ण हैं।

Polygons on the Basis of Shape

बहुभुज को उनके आकार के आधार पर अवतल या उत्तल के रूप में वर्गीकृत किया जा सकता है।

•     एक अवतल बहुभुज एक ऐसा बहुभुज होता है जिसका कम से कम एक आंतरिक कोण 90∘ से बड़ा होता है। बहुभुज जो अवतल होते हैं, उनके बाहरी हिस्से में उनके विकर्णों के कम से कम कुछ भाग होते हैं।
•     एक उत्तल बहुभुज एक बहुभुज है जिसका सभी आंतरिक कोण 180∘ से कम है। बहुभुज जो उत्तल होते हैं, उनके बाहरी भाग में उनके विकर्णों का कोई भाग नहीं होता है।

Polygons on the Basis of Shape

 
 बहुभुजों का उनके आकार के आधार पर वर्गीकरण।

Polygons on the Basis of Regularity

बहुभुज को नियमितता के आधार पर नियमित बहुभुज और अनियमित बहुभुज के रूप में भी वर्गीकृत किया जा सकता है।

•     जब एक बहुभुज समबाहु और समकोणिक दोनों हो तो उसे नियमित बहुभुज कहते हैं। एक सम बहुभुज में, सभी भुजाएँ और सभी कोण समान होते हैं। उदाहरण: स्क्वायर
•     एक बहुभुज जो नियमित नहीं है अर्थात यह समबाहु और समकोण नहीं है, एक अनियमित बहुभुज है। उदाहरण: आयत

Polygons on the Basis of Regularity

understanding quadrilaterals class 8 : Introduction to Quadrilaterals

Angle Sum Property of a Polygon

बहुभुज के कोण योग गुण के अनुसार, बहुभुज के सभी आंतरिक कोणों का योग बराबर होता है (n−2)×180∘, जहां n बहुभुज की भुजाओं की संख्या है।.

 Division of a quadrilateral into two triangles.

 
जैसा कि हम उपरोक्त चतुर्भुज के लिए देख सकते हैं, यदि हम चतुर्भुज के किसी एक विकर्ण को मिलाते हैं, तो हमें दो त्रिभुज प्राप्त होते हैं।
दो त्रिभुजों के सभी आंतरिक कोणों का योग चतुर्भुज के सभी आंतरिक कोणों के योग के बराबर होता है, जो कि 360∘ = (4−2)×180∘ के बराबर होता है।
इसलिए, यदि कोई बहुभुज है जिसकी n भुजाएँ हैं, तो हम (n - 2) गैर-अतिव्यापी त्रिभुज बना सकते हैं जो उस बहुभुज को पूरी तरह से ढक देगा।

Quadrilaterals

बहुभुज के आंतरिक कोणों का योग त्रिभुजों के आंतरिक कोणों के योग के बराबर होगा = (n−2)×180∘

Sum of Measures of Exterior Angles of a Polygon

किसी भी बहुभुज के बाह्य कोणों के मापों का योग 360∘ होता है।

understanding quadrilaterals class 8 Properties of Parallelograms

 

understanding quadrilaterals class 8 Properties of Parallelograms

Elements of a Parallelogram

•     एक समांतर चतुर्भुज में चार भुजाएँ और चार कोण होते हैं।
•     समांतर चतुर्भुज की सम्मुख भुजाएँ और सम्मुख कोण बराबर होते हैं।
•     समांतर चतुर्भुज ABCD में, भुजाएँ AB और CD विपरीत भुजाएँ हैं और भुजाएँ AB और हैं BC आसन्न भुजाएँ हैं।
•     इसी प्रकार, $\angle ABC$ और $\angle ADC$ सम्मुख कोण हैं और $\angle ABC$ और $\angle BCD$ आसन्न कोण हैं।

Angles of a Parallelogram

समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
समांतर चतुर्भुज ABCD में, ∠ABC=∠ADC और DAB=∠BCD।

समांतर चतुर्भुज में आसन्न कोण संपूरक होते हैं।
∴ समांतर चतुर्भुज ABCD में, ABC+∠BCD=∠ADC+∠DAB=180∘
समांतर चतुर्भुज के विकर्ण

एक समांतर चतुर्भुज के विकर्ण एक दूसरे को प्रतिच्छेदन बिंदु पर समद्विभाजित करते हैं।
नीचे दिए गए समांतर चतुर्भुज ABCD में, OA = OC और OB = OD है।

understanding quadrilaterals class 8 Notes :- Properties of Special Parallelograms

Rectangle

एक आयत समान कोणों वाला एक समांतर चतुर्भुज होता है और प्रत्येक कोण 90∘ के बराबर होता है।
गुण:

•     एक आयत की सम्मुख भुजाएँ समानांतर और बराबर होती हैं।
•     एक आयत के विकर्णों की लंबाई बराबर होती है।
•     एक आयत के सभी आंतरिक कोण 90∘ के बराबर होते हैं।
•     एक आयत के विकर्ण एक दूसरे को प्रतिच्छेदन बिंदु पर समद्विभाजित करते हैं।

 

Square

एक वर्ग समान भुजाओं वाला एक आयत है। एक आयत के सभी गुण एक वर्ग के लिए भी सत्य होते हैं।
एक वर्ग में विकर्ण:

•      एक दूसरे को समद्विभाजित करना
•      समान लंबाई के हैं
•      एक दूसरे के लंबवत हैं