NCERT solutions for class 8 maths chapter 2 in hindi - math solution class 8
ncert solutions for class 8 maths chapter 2 pdf लीनियर इक्वेशन इन वन वेरिएबल, यहां पीडीएफ फॉर्मेट में उपलब्ध कराए गए हैं, जिन्हें मुफ्त में डाउनलोड किया जा सकता है। एक चर में चैप्टर लीनियर इक्वेशन के लिए NCERT सॉल्यूशंस को गणित विशेषज्ञों द्वारा सटीक रूप से डिजाइन किया गया है।
एक चर में रैखिक समीकरणों के सभी हल किए गए प्रश्न, नवीनतम एनसीईआरटी पाठ्यक्रम और दिशानिर्देशों के संबंध में हैं, ताकि छात्रों को पुस्तक में मौजूद प्रत्येक अभ्यास प्रश्न को हल करने और परीक्षा की तैयारी में मदद मिल सके।
ये समाधान छात्रों को अपना होमवर्क और असाइनमेंट करने के लिए एक संदर्भ उपकरण के रूप में भी काम करते हैं।
कक्षा 8 के एनसीईआरटी समाधान में सभी अध्यायों के लिए अभ्यास-वार उत्तर शामिल हैं, इस प्रकार कक्षा 8 में पढ़ने वाले छात्रों के लिए एक बहुत ही उपयोगी अध्ययन सामग्री है। इन समाधानों का अभ्यास करने से छात्रों को अंतिम परीक्षा में टॉप करने और विषय को बेहतर बनाने में मदद मिलती है।
ये समाधान सबसे अद्यतन एनसीईआरटी पाठ्यक्रम के आधार पर तैयार किए गए हैं, जिसमें संबंधित विषयों के सभी महत्वपूर्ण विषयों को शामिल किया गया है।
ncert solutions for class 8 maths chapter 2
व्यायाम 2.1 पृष्ठ: 23
निम्नलिखित समीकरणों को हल कीजिए।
1. एक्स - 2 = 7
समाधान:
एक्स - 2 = 7
एक्स=7+2
एक्स = 9
2. वाई + 3 = 10
समाधान:
वाई + 3 = 10
वाई = 10 -3
वाई = 7
3. 6 = जेड + 2
समाधान:
6 = जेड + 2
जेड + 2 = 6
जेड = 6-2
जेड = 4
4. 3/7 + x = 17/7
समाधान:
3/7 + x = 17/7
एक्स = 17/7 - 3/7
एक्स = 14/7
एक्स = 2
5. 6x = 12
समाधान:
6x = 12
एक्स = 12/6
एक्स = 2
6. टी/5 = 10
समाधान:
टी/5 = 10
टी = 10 × 5
टी = 50
7. 2x/3 = 18
समाधान:
2x/3 = 18
2x = 18 × 3
2x = 54
एक्स = 54/2
एक्स = 27
8. 1.6 = वाई/15
समाधान:
1.6 = y/1.5
वाई/1.5 = 1.6
वाई = 1.6 × 1.5
वाई = 2.4
9. 7x - 9 = 16
समाधान:
7x - 9 = 16
7x = 16+9
7x = 25
एक्स = 25/7
10. 14y - 8 = 13
समाधान:
14y - 8 = 13
14y = 13+8
14y = 21
वाई = 21/14
वाई = 3/2
11. 17 + 6p = 9
समाधान:
17 + 6पी = 9
6पी = 9 - 17
6p = -8
पी = -8/6
पी = -4/3
12. x/3 + 1 = 7/15
समाधान:
एक्स/3 + 1 = 7/15
एक्स/3 = 7/15 - 1
एक्स/3 = (7 -15)/15
एक्स/3 = -8/15
एक्स = -8/15 × 3
एक्स = -8/5
ncert solutions for class 8 maths chapter 2 - Exercise 2.2
1. यदि आप किसी संख्या में से ½ घटाते हैं और परिणाम को ½ से गुणा करते हैं, तो आपको 1/8 मिलता है, वह संख्या क्या है?
समाधान:
माना संख्या x है।
प्रश्न के अनुसार,
(x - 1/2) × ½ = 1/8
एक्स/2 - = 1/8
एक्स/2 = 1/8 +
एक्स/2 = 1/8 + 2/8
एक्स/2 = (1+ 2)/8
एक्स/2 = 3/8
एक्स = (3/8) × 2
एक्स = 3/4
2. एक आयताकार स्विमिंग पूल का परिमाप 154 मीटर है। इसकी लंबाई इसकी चौड़ाई के दोगुने से 2 मीटर अधिक है। पूल की लंबाई और चौड़ाई क्या है?
समाधान:
मान लीजिये,
आयताकार स्विमिंग पूल का परिमाप = 154 मीटर माना आयत की चौड़ाई = x
प्रश्न के अनुसार,
आयत की लंबाई = 2x + 2 हम जानते हैं कि,
परिमाप = 2 (लंबाई + चौड़ाई)
⇒ 2(2x + 2 + x) = 154 वर्ग मीटर
2(3x + 2) = 154
3x +2 = 154/2
⇒ 3x = 77 - 2
3x = 75
⇒ एक्स = 75/3
⇒ एक्स = 25 एम
इसलिए, चौड़ाई = x = 25 सेमी
लंबाई = 2x + 2
= (2 × 25) + 2
= 50 + 2
= 52 वर्ग मीटर
3. एक समद्विबाहु त्रिभुज का आधार 4/3 सेमी है। त्रिभुज का परिमाप 4*2/15मी है। शेष समान भुजाओं में से किसी एक की लंबाई क्या है?
समाधान:
समद्विबाहु त्रिभुज का आधार = 4/3 सेमी
त्रिभुज का परिमाप =
ncert solutions for class 8 maths chapter 2
माना त्रिभुज की समान भुजाओं की लंबाई x है।
प्रश्न के अनुसार,
4/3 + x + x = 62/15 सेमी
⇒ 2x = (62/15 - 4/3) सेमी
⇒ 2x = (62 – 20)/15 सेमी
⇒ 2x = 42/15 सेमी
⇒ एक्स = (42/30) × (½)
⇒ एक्स = 42/30 सेमी
⇒ एक्स = 7/5 सेमी
शेष समान भुजाओं में से किसी एक की लंबाई 7/5 सेमी है।
4. दो संख्याओं का योग 95 है। यदि एक संख्या दूसरी से 15 अधिक है, तो संख्याएँ ज्ञात कीजिए।
समाधान:
माना संख्याओं में से एक = x है।
फिर, प्रश्न के अनुसार दूसरी संख्या x + 15 हो जाती है,
एक्स + एक्स + 15 = 95
⇒ 2x + 15 = 95
2x = 95 - 15
2x = 80
एक्स = 80/2
एक्स = 40
पहली संख्या = x = 40
और, दूसरी संख्या = x + 15 = 40 + 15 = 55
5. दो संख्याएँ 5:3 के अनुपात में हैं। यदि वे 18 से भिन्न हैं, तो संख्याएँ क्या हैं?
समाधान:
माना कि दो संख्याएँ 5x और 3x हैं। प्रश्न के अनुसार,
5x - 3x = 18
⇒ 2x = 18
एक्स = 18/2
एक्स = 19
इस प्रकार,
संख्याएँ हैं 5x = 5 × 9 = 45
और 3x = 3 × 9 = 27.
6. तीन क्रमागत पूर्णांकों का योग 51 होता है। ये पूर्णांक क्या हैं?
समाधान:
मान लीजिए कि तीन क्रमागत पूर्णांक x, x+1 और x+2 हैं। प्रश्न के अनुसार,
एक्स + (एक्स+1) + (एक्स+2) = 51
3x + 3 = 51
3x = 51 - 3
⇒ 3x = 48
एक्स = 48/3
एक्स = 16
इस प्रकार, पूर्णांक हैं
एक्स = 16
एक्स + 1 = 17
एक्स + 2 = 18
7. 8 के तीन क्रमागत गुणजों का योग 888 है। गुणज ज्ञात कीजिए।
समाधान:
माना 8 के लगातार तीन गुणज 8x, 8(x+1) और 8(x+2) हैं। प्रश्न के अनुसार,
8x + 8(x+1) + 8(x+2) = 888
⇒ 8 (x + x+1 + x+2) = 888 (8 को सामान्य मानकर)
8 (3x + 3) = 888
3x + 3 = 888/8
⇒ 3x + 3 = 111
⇒ 3x = 111 - 3
3x = 108
एक्स = 108/3
एक्स = 36
इस प्रकार, 8 के लगातार तीन गुणज हैं:
8x = 8 × 36 = 288
8(x + 1) = 8 × (36 + 1) = 8 × 37 = 296
8(x + 2) = 8 × (36 + 2) = 8 × 38 = 304
8. तीन क्रमागत पूर्णांक ऐसे हैं कि जब उन्हें बढ़ते क्रम में लिया जाता है और क्रमशः 2, 3 और 4 से गुणा किया जाता है, तो वे 74 तक जुड़ जाते हैं। इन संख्याओं को खोजें।
समाधान:
माना कि तीन क्रमागत पूर्णांक x, x+1 और x+2 हैं। प्रश्न के अनुसार,
2x + 3(x+1) + 4(x+2) = 74
⇒ 2x + 3x +3 + 4x + 8 = 74
9x + 11 = 74
9x = 74 - 11
⇒ 9x = 63
एक्स = 63/9
एक्स = 7
इस प्रकार, संख्याएँ हैं:
एक्स = 7
एक्स + 1 = 8
एक्स + 2 = 9
9. राहुल और हारून की आयु का अनुपात 5:7 है। चार वर्ष बाद उनकी आयु का योग 56 वर्ष होगा। उनकी वर्तमान आयु क्या है?
समाधान:
माना राहुल और हारून की आयु 5x और 7x है। चार साल बाद,
राहुल और हारून की आयु क्रमशः (5x + 4) और (7x + 4) होगी। प्रश्न के अनुसार,
(5x + 4) + (7x + 4) = 56
⇒ 5x + 4 + 7x + 4 = 56
12x + 8 = 56
12x = 56 - 8
12x = 48
एक्स = 48/12
एक्स = 4
इसलिए, राहुल की वर्तमान आयु = 5x = 5×4 = 20
और, हारून की वर्तमान आयु = 7x = 7×4 = 28
10. एक कक्षा में लड़कों और लड़कियों की संख्या का अनुपात 7:5 है। लड़कों की संख्या लड़कियों की संख्या से 8 अधिक है। कुल वर्ग शक्ति क्या है?
समाधान:
माना लड़कों की संख्या 7x और लड़कियों की संख्या 5x है।
प्रश्न के अनुसार,
7x = 5x + 8
7x - 5x = 8
⇒ 2x = 8
एक्स = 8/2
एक्स = 4
अत: लड़कों की संख्या = 7×4 = 28
और, लड़कियों की संख्या = 5×4 = 20
छात्रों की कुल संख्या = 20+28 = 48
11. बाइचुंग के पिता बाइचुंग के दादा से 26 साल छोटे और बाइचुंग से 29 साल बड़े हैं। तीनों की आयु का योग 135 वर्ष है। उनमें से प्रत्येक की आयु क्या है?
समाधान:
माना बाइचुंग के पिता की आयु x है।
तो, बाइचुंग के दादा की आयु = (x+26)
और, बाइचुंग की आयु = (x-29) प्रश्न के अनुसार,
एक्स + (एक्स+26) + (एक्स-29) = 135
3x + 26 - 29 = 135
3x - 3 = 135
3x = 135 + 3
3x = 138
एक्स = 138/3
एक्स = 46
बाइचुंग के पिता की आयु = x = 46
बाइचुंग के दादा की आयु = (x+26) = 46 + 26 = 72
बाइचुंग की आयु = (x-29) = 46 - 29 = 17
12. अब से पंद्रह वर्ष बाद रवि की आयु उसकी वर्तमान आयु की चार गुना होगी। रवि की वर्तमान आयु क्या है?
समाधान:
माना रवि की वर्तमान आयु x है।
पंद्रह वर्ष बाद, रवि की आयु x+15 वर्ष होगी। प्रश्न के अनुसार,
एक्स + 15 = 4x
4x - x = 15
3x = 15
⇒ एक्स = 15/3
एक्स = 5
अत: रवि की वर्तमान आयु = 5 वर्ष।
13. एक परिमेय संख्या ऐसी होती है कि जब आप इसे 5/2 से गुणा करते हैं और गुणनफल में 2/3 जोड़ते हैं, तो आपको -7/12 प्राप्त होता है। संख्या क्या है?
समाधान:
माना परिमेय x है।
प्रश्न के अनुसार,
एक्स × (5/2) + 2/3 = -7/12
5x/2 + 2/3 = -7/12
5x/2 = -7/12 - 2/3
⇒ 5x/2 = (-7- 8)/12
5x/2 = -15/12
⇒ 5x/2 = -5/4
⇒ एक्स = (-5/4) × (2/5)
एक्स = - 10/20
एक्स = -½
अत: परिमेय संख्या -½ है।
14. लक्ष्मी एक बैंक में खजांची है। उसके पास क्रमशः ₹100, ₹50 और ₹10 मूल्यवर्ग के करेंसी नोट हैं। इन नोटों की संख्या का अनुपात 2:3:5 है। लक्ष्मी के पास कुल नकद ₹4,00,000 है। उसके पास प्रत्येक संप्रदाय के कितने नोट हैं?
समाधान:
माना ₹100, ₹50 और ₹10 के नोटों की संख्या क्रमश: 2x, 3x और 5x है।
₹100 का मूल्य = 2x × 100 = 200x
₹50 का मूल्य = 3x × 50 = 150x
₹10 का मूल्य = 5x × 10 = 50x प्रश्न के अनुसार,
200x + 150x + 50x = 4,00,000
400x = 4,00,000
एक्स = 400000/400
एक्स = 1000
₹100 के नोटों की संख्या = 2x = 2000
₹50 के नोटों की संख्या = 3x = 3000
₹10 के नोटों की संख्या = 5x = 5000
15. मेरे पास ₹1, ₹2 और ₹5 मूल्य के सिक्कों में कुल ₹300 हैं। ₹2 के सिक्कों की संख्या ₹5 के सिक्कों की संख्या की 3 गुनी है। सिक्कों की कुल संख्या 160 है। मेरे पास प्रत्येक मूल्यवर्ग के कितने सिक्के हैं?
समाधान:
माना ₹5 के सिक्कों की संख्या x है।
फिर,
संख्या ₹2 के सिक्के = 3x
और, ₹1 के सिक्कों की संख्या = (160 - 4x) अब,
₹5 के सिक्कों का मूल्य = x × 5 = 5x
₹2 के सिक्कों का मूल्य = 3x × 2 = 6x
₹1 के सिक्कों का मूल्य = (160 - 4x) × 1 = (160 - 4x)
प्रश्न के अनुसार,
5x + 6x + (160 - 4x) = 300
⇒ 11x + 160 - 4x = 300
7x = 140
⇒ एक्स = 140/7
एक्स = 20
₹5 के सिक्कों की संख्या = x = 20
₹2 के सिक्कों की संख्या = 3x = 60
₹1 के सिक्कों की संख्या = (160 - 4x) = 160 - 80 = 80
16. एक निबंध प्रतियोगिता के आयोजक यह निर्णय लेते हैं कि प्रतियोगिता में विजेता को ₹100 का पुरस्कार मिलेगा और जो प्रतिभागी नहीं जीतेगा उसे ₹25 का पुरस्कार मिलेगा। वितरित की गई कुल पुरस्कार राशि ₹3,000 है। विजेताओं की संख्या ज्ञात कीजिए, यदि प्रतिभागियों की कुल संख्या 63 है।
समाधान:
माना विजेताओं की संख्या x है।
फिर, न जीतने वाले प्रतिभागियों की संख्या = 63 - x
विजेता को दिया गया कुल पैसा = x × 100 = 100x
जीतने वाले प्रतिभागी को दिया गया कुल पैसा = 25×(63-x)
प्रश्न के अनुसार,
100x + 25×(63-x) = 3,000
100x + 1575 - 25x = 3,000
75x = 3,000 - 1575
75x = 1425
एक्स = 1425/75
एक्स = 19
अतः विजेताओं की संख्या 19 है।
class 8 maths chapter 2 exercise 2.3 solutions : page: 30
निम्नलिखित समीकरणों को हल करें और अपने परिणामों की जाँच करें।
1. 3x = 2x + 18
समाधान:
3x = 2x + 18
3x - 2x = 18
एक्स = 18
RHS और LHS में x का मान रखने पर हमें प्राप्त होता है, 3 × 18 = (2 × 18) +18
54 = 54
⇒ एलएचएस = आरएचएस
2. 5t - 3 = 3t - 5
समाधान:
5t - 3 = 3t - 5
5t - 3t = -5 + 3
2t = -2
टी = -1
RHS और LHS में t का मान रखने पर, 5× (-1) – 3 = 3× (-1) – 5 प्राप्त होता है।
-5 - 3 = -3 - 5
-8 = -8
⇒ एलएचएस = आरएचएस
3. 5x + 9 = 5 + 3x
समाधान:
5x + 9 = 5 + 3x
5x - 3x = 5 - 9
⇒ 2x = -4
⇒ एक्स = -2
RHS और LHS में x का मान रखने पर हमें प्राप्त होता है, 5× (-2) + 9 = 5 + 3× (-2)
-10 + 9 = 5 + (-6)
-1 = -1
⇒ एलएचएस = आरएचएस
4. 4z + 3 = 6 + 2z
समाधान:
4z + 3 = 6 + 2z
4z - 2z = 6 - 3
2z = 3
जेड = 3/2
RHS और LHS में z का मान रखने पर, हमें प्राप्त होता है,
(4 × 3/2) + 3 = 6 + (2 × 3/2)
6 + 3 = 6 + 3
9 = 9
⇒ एलएचएस = आरएचएस
5. 2x - 1 = 14 - x
समाधान:
2x - 1 = 14 - x
⇒ 2x + x = 14 + 1
3x = 15
एक्स = 5
RHS और LHS में x का मान रखने पर हमें प्राप्त होता है, (2×5) – 1 = 14 – 5
10 - 1 = 9
9 = 9
⇒ एलएचएस = आरएचएस
6. 8x + 4 = 3 (x - 1) + 7
समाधान:
8x + 4 = 3 (x - 1) + 7
⇒ 8x + 4 = 3x - 3 + 7
⇒ 8x + 4 = 3x + 4
⇒ 8x - 3x = 4 - 4
⇒ 5x = 0
एक्स = 0
RHS और LHS में x का मान रखने पर, (8×0) + 4 = 3 (0 – 1) + 7 . प्राप्त होता है
0 + 4 = 0 - 3 + 7
4 = 4
⇒ एलएचएस = आरएचएस
7. एक्स = 4/5 (एक्स + 10)
समाधान:
एक्स = 4/5 (एक्स + 10)
एक्स = 4x/5 + 40/5
⇒ एक्स - (4x/5) = 8
(5x - 4x)/5 = 8
एक्स = 8 × 5
एक्स = 40
RHS और LHS में x का मान रखने पर, हमें प्राप्त होता है,
40 = 4/5 (40 + 10)
40 = 4/5 × 50
40 = 200/5
40 = 40
⇒ एलएचएस = आरएचएस
8. 2x/3 + 1 = 7x/15 + 3
समाधान:
2x/3 + 1 = 7x/15 + 3
⇒ 2x/3 - 7x/15 = 3 - 1
(10x - 7x)/15 = 2
3x = 2 × 15
3x = 30
एक्स = 30/3
एक्स = 10
RHS और LHS में x का मान रखने पर, हमें प्राप्त होता है,
9. 2y + 5/3 = 26/3 - y
समाधान:
2y + 5/3 = 26/3 - y
2y + y = 26/3 - 5/3
3y = (26 - 5)/3
3y = 21/3
3y = 7
वाई = 7/3
RHS और LHS में y का मान रखने पर,
(2 × 7/3) + 5/3 = 26/3 - 7/3
⇒ 14/3 + 5/3 = 26/3 - 7/3
(14 + 5)/3 = (26 - 7)/3
19/3 = 19/3
⇒ एलएचएस = आरएचएस
10. 3मी = 5मी - 8/5
समाधान:
3मी = 5मी - 8/5
5मी - 3मी = 8/5
⇒ 2m = 8/5
⇒ 2m × 5 = 8
10 मी = 8
एम = 8/10
⇒ एम = 4/5
RHS और LHS में m का मान रखने पर,
3 × (4/5) = (5 × 4/5) - 8/5
12/5 = 4 - (8/5)
12/5 = (20 - 8)/5
12/5 = 12/5
⇒ एलएचएस = आरएचएस
ncert solutions for class 8 maths chapter 2 : Exercise - 2.4
1. अमीना एक संख्या के बारे में सोचती है और उसमें से 5/2 घटाती है। वह परिणाम को 8 से गुणा करती है। अब प्राप्त परिणाम उसी संख्या का 3 गुना है जिसके बारे में उसने सोचा था। संख्या क्या है?
समाधान:
माना संख्या x है,
प्रश्न के अनुसार,
(एक्स - 5/2) × 8 = 3x
⇒ 8x - 40/2 = 3x
⇒ 8x - 3x = 40/2
5x = 20
एक्स = 4
इस प्रकार, संख्या 4 है।
2. एक धनात्मक संख्या दूसरी संख्या का 5 गुना है। यदि दोनों संख्याओं में 21 जोड़ दिया जाए, तो एक नई संख्या दूसरी नई संख्या से दोगुनी हो जाती है। संख्याएं क्या हैं?
समाधान:
माना एक धनात्मक संख्या x है तो दूसरी संख्या 5x होगी। प्रश्न के अनुसार,
5x + 21 = 2 (x + 21)
⇒ 5x + 21 = 2x + 42
5x - 2x = 42 - 21
3x = 21
एक्स = 7
एक संख्या = x = 7
अन्य संख्या = 5x = 5x7 = 35 दो संख्याएँ 7 और 35 हैं।
3. दो अंकों की संख्या के अंकों का योग 9 है। जब हम अंकों को आपस में बदलते हैं, तो यह पाया जाता है कि परिणामी नई संख्या मूल संख्या से 27 अधिक है। दो अंकों की संख्या क्या है?
समाधान:
माना दहाई के स्थान का अंक x है तो इकाई के स्थान का अंक (9-x) होगा।
मूल दो अंकों की संख्या = 10x + (9-x)
अंकों को आपस में बदलने के बाद, नई संख्या = 10(9-x) + x
प्रश्न के अनुसार,
10x + (9-x) + 27 = 10(9-x) + x
10x + 9 - x + 27 = 90 - 10x + x
9x + 36 = 90 - 9x
⇒ 9x + 9x = 90 - 36
⇒ 18x = 54
एक्स = 3
मूल संख्या = 10x + (9-x) = (10×3) + (9-3) = 30 + 6 = 36
अत: संख्या 36 है।
4. दो अंकों की एक संख्या के दो अंकों में से एक अंक दूसरे अंक का तीन गुना होता है। यदि आप इस दो अंकों की संख्या के अंकों को आपस में बदल दें और परिणामी संख्या को मूल संख्या में जोड़ दें, तो आपको 88 प्राप्त होता है। मूल संख्या क्या है?
समाधान:
माना दहाई के स्थान का अंक x है तो इकाई के स्थान का अंक 3x होगा।
मूल दो अंकों की संख्या = 10x + 3x
अंकों को आपस में बदलने के बाद, नई संख्या = 30x + x
प्रश्न के अनुसार,
(30x + x) + (10x + 3x) = 88
31x + 13x = 88
44x = 88
एक्स = 2
मूल संख्या = 10x + 3x = 13x = 13x2 = 26
5. शोबो की माँ की वर्तमान आयु शोबो की वर्तमान आयु की छह गुना है। अब से पांच वर्ष बाद शोबो की आयु उसकी माता की वर्तमान आयु की एक तिहाई होगी। उनकी वर्तमान आयु क्या है?
समाधान:
माना शोबो की वर्तमान आयु x है तो उसकी माता की आयु 6x होगी।
5 वर्ष बाद शोबो की आयु = x + 5
प्रश्न के अनुसार,
(एक्स + 5) = (1/3) × 6x
एक्स + 5 = 2x
⇒ 2x - x = 5
एक्स = 5
शोबो की वर्तमान आयु = x = 5 वर्ष
शोबो की माँ की वर्तमान आयु = 6x = 30 वर्ष।
6. माहुली गांव में एक संकीर्ण आयताकार भूखंड एक स्कूल के लिए आरक्षित है। प्लॉट की लंबाई और चौड़ाई 11:4 के अनुपात में है। ₹100 प्रति मीटर की दर से ग्राम पंचायत को प्लॉट की बाड़ लगाने के लिए ₹75000 खर्च होंगे। साजिश के आयाम क्या हैं?
समाधान:
माना आयताकार भूखंड की लंबाई 11x और चौड़ाई 4x है।
बाड़ लगाने की दर प्रति मीटर = ₹100
बाड़ लगाने की कुल लागत = ₹75000
भूखंड का परिमाप = 2(l+b) = 2(11x + 4x) = 2×15x = 30x
बाड़ लगाने की कुल राशि = (30x × 100)
प्रश्न के अनुसार,
(30x × 100) = 75000
3000x = 75000
एक्स = 75000/3000
एक्स = 25
प्लॉट की लंबाई = 11x = 11 × 25 = 275m
भूखंड की चौड़ाई = 4 × 25 = 100 मी।
7. हसन स्कूल यूनिफॉर्म के लिए दो तरह की कपड़ा सामग्री खरीदता है, शर्ट की सामग्री जिसकी कीमत उसके लिए ₹50 प्रति मीटर है और पतलून की सामग्री जिसकी कीमत ₹90 प्रति मीटर है। शर्ट सामग्री के प्रत्येक 3 मीटर के लिए वह 2 मीटर पतलून सामग्री खरीदता है। वह सामग्री को क्रमशः 12% और 10% लाभ पर बेचता है। उनकी कुल बिक्री ₹36,600 है। उसने कितनी पतलून सामग्री खरीदी?
समाधान:
माना 2x मीटर पतलून सामग्री और 3x मीटर शर्ट सामग्री उसके द्वारा खरीदी गई
शर्ट सामग्री का प्रति मीटर विक्रय मूल्य = ₹ 50 + 50 × (12/100) = ₹ 56
पतलून सामग्री का प्रति मीटर विक्रय मूल्य = ₹ 90 + 90 × (10/100) = ₹ 99
बिक्री की कुल राशि = ₹36,600
प्रश्न के अनुसार,
(2x × 99) + (3x × 56) = 36600
⇒ 198x + 168x = 36600
⇒ 366x = 36600
⇒ एक्स = 36600/366
एक्स = 100
उसके द्वारा खरीदी गई पतलून की कुल सामग्री = 2x = 2 × 100 = 200 मी।
8. हिरणों के एक झुण्ड का आधा भाग खेत में चर रहा है और शेष का तीन चौथाई पास में खेल रहा है। बाकी 9 तालाब का पानी पी रहे हैं। झुंड में हिरणों की संख्या ज्ञात कीजिए।
समाधान:
माना हिरणों की कुल संख्या x है।
मैदान में चरना हिरण = x/2
पास में खेलने वाला हिरण = x/2 × = 3x/8
मृग पीने का पानी = 9
प्रश्न के अनुसार,
x/2 + 3x/8 + 9 = x
(4x + 3x)/8 + 9 = x
7x/8 + 9 = x
एक्स - 7x/8 = 9
(8x - 7x)/8 = 9
एक्स = 9 × 8
एक्स = 72
9. एक दादा अपनी पोती से दस गुना बड़ा है। वह भी उनसे 54 साल बड़े हैं। उनकी वर्तमान आयु ज्ञात कीजिए।
समाधान:
माना पोती की आयु x और दादा की आयु 10x है।
साथ ही वह उनसे 54 साल बड़े हैं।
प्रश्न के अनुसार, 10x = x + 54
10x - x = 54
⇒ 9x = 54
एक्स = 6
दादाजी की आयु = 10x = 10x6 = 60 वर्ष।
पोती की आयु = x = 6 वर्ष।
10. अमन की आयु उसके पुत्र की आयु की तीन गुनी है। दस साल पहले वह अपने बेटे की उम्र का पांच गुना था। उनकी वर्तमान आयु ज्ञात कीजिए।
समाधान:
माना अमन के पुत्र की आयु x है तो अमन की आयु 3x होगी।
प्रश्न के अनुसार,
5(x - 10) = 3x - 10
5x - 50 = 3x - 10
⇒ 5x - 3x = -10 + 50
⇒ 2x = 40
एक्स = 20
अमन के पुत्र की आयु = x = 20 वर्ष
अमन की उम्र = 3x = 3×20 = 60 साल
ncert solutions for class 8 maths chapter 2 - Exercise 2.5
निम्नलिखित रैखिक समीकरणों को हल करें।
1. x/2 - 1/5 = x/3 +
समाधान:
x/2 - 1/5 = x/3 +
एक्स/2 - एक्स/3 = ¼+ 1/5
(3x - 2x)/6 = (5 + 4)/20
3x - 2x = 9/20 × 6
एक्स = 54/20
एक्स = 27/10
2. एन/2 - 3एन/4 + 5एन/6 = 21
समाधान:
एन/2 - 3एन/4 + 5एन/6 = 21
(6n - 9n + 10n)/12 = 21
7n/12 = 21
7n = 21 × 12
एन = 252/7
एन = 36
3. x + 7 - 8x / 3 = 17/6 - 5x / 2
समाधान:
x + 7 – 8x/3 = 17/6 – 5x/2
x - 8x/3 + 5x/2 = 17/6 - 7
⇒ (6x - 16x + 15x)/6 = (17 - 42)/6
5x/6 = - 25/6
5x = - 25
एक्स = - 5
4. (x - 5)/3 = (x - 3)/5
समाधान:
(एक्स - 5) / 3 = (एक्स - 3) / 5
⇒ 5(x-5) = 3(x-3)
5x-25 = 3x-9
5x - 3x = -9+25
⇒ 2x = 16
एक्स = 8
5. (3t – 2)/4 – (2t + 3)/3 = 2/3 – t
समाधान:
(3t – 2)/4 – (2t + 3)/3 = 2/3 – t
((3t - 2)/4) × 12 - ((2t + 3)/3) × 12
(3t – 2) × 3 – (2t + 3) × 4 = 2 × 4 – 12t
9t - 6 - 8t - 12 = 8 - 12t
9t - 6 - 8t - 12 = 8 - 12t
टी - 18 = 8 - 12 टी
टी + 12 टी = 8 + 18
13टी = 26
टी = 2
6. एम - (एम -1)/2 = 1 - (एम - 2)/3
समाधान:
एम - (एम -1)/2 = 1 - (एम - 2)/3
⇒ एम - एम / 2 - 1/2 = 1 - (एम / 3 - 2/3)
एम - एम/2 + ½ = 1 - एम/3 + 2/3
⇒ एम - एम/2 + एम/3 = 1 + 2/3 - ½
⇒ एम/2 + एम/3 = ½ + 2/3
⇒ (3मी + 2मी)/6 = (3 + 4)/6
⇒ 5m/6 = 7/6
एम = 7/6 × 6/5
⇒ एम = 7/5
निम्नलिखित रैखिक समीकरणों को सरल कीजिए और हल कीजिए।
7. 3(t - 3) = 5(2t + 1)
समाधान:
3(टी – 3) = 5(2टी + 1)
3t - 9 = 10t + 5
3t - 10t = 5 + 9
-7t = 14
टी = 14/-7
टी = -2
8. 8. 15(y - 4) -2(y - 9) + 5(y + 6) = 0
समाधान:
15(y – 4) –2(y – 9) + 5(y + 6) = 0
⇒ 15y - 60 -2y + 18 + 5y + 30 = 0
15y - 2y + 5y = 60 - 18 - 30
18वाई = 12
वाई = 12/18
वाई = 2/3
9. 3(5z - 7) - 2(9z - 11) = 4(8z - 13) - 17
समाधान:
3(5z - 7) - 2(9z - 11) = 4(8z - 13) - 17
⇒ 15z - 21 - 18z + 22 = 32z - 52 - 17
15z - 18z - 32z = -52 - 17 + 21 - 22
-35z = -70
जेड = -70/-35
जेड = 2
10. 0.25(4f - 3) = 0.05(10f - 9)
समाधान:
0.25(4f - 3) = 0.05(10f - 9)
⇒ एफ - 0.75 = 0.5 एफ - 0.45
⇒ एफ - 0.5 एफ = -0.45 + 0.75
⇒ 0.5f = 0.30
एफ = 0.30/0.5
एफ = 3/5
एफ = 0.6
व्यायाम 2.6 पृष्ठ: 35
निम्नलिखित समीकरणों को हल कीजिए।
1. (8x - 3)/3x = 2
समाधान:
(8x - 3)/3x = 2
⇒ 8x/3x - 3/3x = 2
8/3 - 1/x = 2
⇒ 8/3 - 2 = 1/x
(8 - 6)/3 = 1/x
⇒ 2/3 = 1/x
एक्स = 3/2
2. 9x/(7 - 6x) = 15
समाधान:
9x/(7 - 6x) = 15
⇒ 9x = 15 (7 - 6x)
9x = 105 - 90x
9x + 90x = 105
99x = 105
एक्स = 105/99 = 35/33
3. z/(z + 15) = 4/9
समाधान:
जेड/(जेड + 15) = 4/9
जेड = 4/9 (जेड + 15)
9z = 4(z + 15)
9z = 4z + 60
9z - 4z = 60
5z = 60
जेड = 12
4. (3y + 4)/(2 - 6y) = -2/5
समाधान:
(3y + 4)/(2 - 6y) = -2/5
3y + 4 = -2/5 (2 - 6y)
5(3y + 4) = -2(2 - 6y)
⇒ 15y + 20 = -4 + 12y
15y - 12y = -4 - 20
3y = -24
वाई = -8
5. (7y + 4)/(y + 2) = -4/3
समाधान:
(7y + 4)/(y + 2) = -4/3
7y + 4 = -4/3 (y + 2)
3(7y + 4) = -4(y + 2)
21y + 12 = -4y - 8
⇒ 21y + 4y = -8 - 12
⇒ 25y = -20
वाई = -20/25 = -4/5
6. हरि और हैरी की आयु का अनुपात 5:7 है। अब से चार वर्ष बाद उनकी आयु का अनुपात 3:4 हो जाएगा। उनकी वर्तमान आयु ज्ञात कीजिए।
समाधान:
माना हरि की आयु 5x और हैरी की आयु 7x है। चार साल बाद,
हरि की आयु = 5x + 4 हैरी की आयु = 7x + 4
प्रश्न के अनुसार,
(5x + 4)/(7x + 4) =
⇒ 4(5x + 4) = 3(7x + 4)
20x + 16 = 21x + 12
⇒ 21x - 20x = 16 - 12
एक्स = 4
हरि आयु = 5x = 5 × 4 = 20 वर्ष
हैरी की उम्र = 7x = 7 × 4 = 28 साल
7. एक परिमेय संख्या का हर उसके अंश से 8 अधिक होता है। यदि अंश में 17 की वृद्धि होती है और हर में 1 की कमी होती है, तो प्राप्त संख्या 3/2 होती है। परिमेय संख्या ज्ञात कीजिए।
समाधान:
माना अंश x है तो हर होगा (x + 8)
प्रश्न के अनुसार,
(एक्स + 17)/(एक्स + 8 – 1) = 3/2
(एक्स + 17)/(एक्स + 7) = 3/2
⇒ 2(x + 17) = 3(x + 7)
⇒ 2x + 34 = 3x + 21
34 - 21 = 3x - 2x
13 = एक्स
परिमेय संख्या x/(x + 8) = 13/21 . है


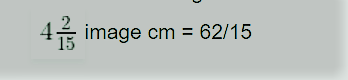








No comments:
Post a Comment