ncert solutions for class 8 maths chapter 3 in Hindi - ncert math solution class 8

 NCERT Solutions for Class 8 Maths Chapter 3 चतुर्भुज को समझना, यहाँ उपलब्ध कराए गए हैं, जिन्हें PDF फॉर्मेट में मुफ्त में डाउनलोड किया जा सकता है। एनसीईआरटी सॉल्यूशंस फॉर चैप्टर अंडरस्टैंडिंग क्वाड्रिलेटर्स परीक्षा के दृष्टिकोण को ध्यान में रखते हुए BYJU'S के गणित विशेषज्ञों द्वारा तैयार किए गए हैं। ये समाधान समस्याओं को हल करने की सटीक विधि बताते हैं। कक्षा 8 के लिए एनसीईआरटी समाधान में प्रयुक्त अवधारणाओं को समझकर, छात्र चतुर्भुज को समझने से संबंधित अपने सभी संदेहों को दूर करने में सक्षम होंगे।

NCERT Solutions for Class 8 Maths Chapter 3 चतुर्भुज को समझना, यहाँ उपलब्ध कराए गए हैं, जिन्हें PDF फॉर्मेट में मुफ्त में डाउनलोड किया जा सकता है। एनसीईआरटी सॉल्यूशंस फॉर चैप्टर अंडरस्टैंडिंग क्वाड्रिलेटर्स परीक्षा के दृष्टिकोण को ध्यान में रखते हुए गणित विशेषज्ञों द्वारा तैयार किए गए हैं। ये समाधान समस्याओं को हल करने की सटीक विधि बताते हैं। कक्षा 8 के लिए एनसीईआरटी समाधान में प्रयुक्त अवधारणाओं को समझकर, छात्र चतुर्भुज को समझने से संबंधित अपने सभी संदेहों को दूर करने में सक्षम होंगे।

ncert solutions for class 8 maths chapter 3

व्यायाम 3.1 पृष्ठ: 41

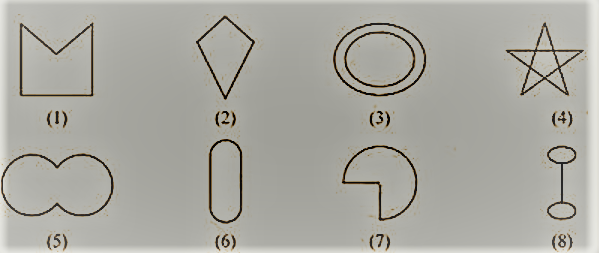
1. यहां कुछ आंकड़े दिए गए हैं।

ncert solutions for class 8 maths chapter 3

निम्नलिखित के आधार पर उनमें से प्रत्येक का वर्गीकरण कीजिए।

सरल वक्र (बी) सरल बंद वक्र (सी) बहुभुज

(डी) उत्तल बहुभुज (ई) अवतल बहुभुज

समाधान:

क) सरल वक्र: 1, 2, 5, 6 और 7

बी) सरल बंद वक्र: 1, 2, 5, 6 और 7

ग) बहुभुज: 1 और 2

डी) उत्तल बहुभुज: 2

ई) अवतल बहुभुज: 1

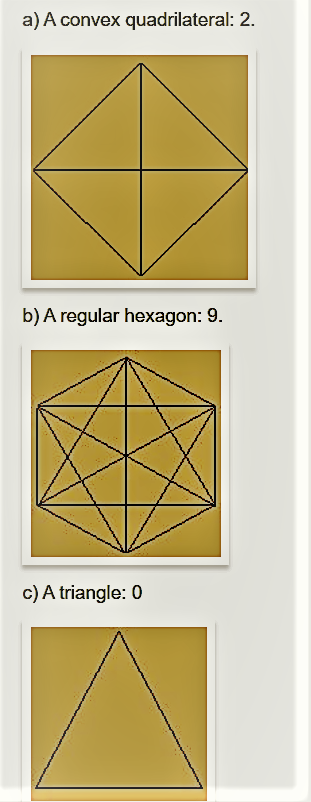
2. निम्नलिखित में से प्रत्येक के कितने विकर्ण हैं?

a) एक उत्तल चतुर्भुज (b) एक नियमित षट्भुज (c) एक त्रिभुज

understanding quadrilaterals class 8 solutions pdf

समाधान:

a) एक उत्तल चतुर्भुज: 2.

3. एक उत्तल चतुर्भुज के कोणों के मापों का योग कितना होता है? यदि चतुर्भुज उत्तल नहीं है तो क्या यह गुण धारण करेगा? (एक गैर-उत्तल चतुर्भुज बनाएं और कोशिश करें!)

ncert solutions for class 8 maths chapter 3

समाधान:

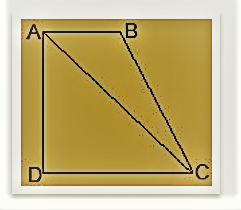
मान लीजिए ABCD एक उत्तल चतुर्भुज है।

आकृति से, हम अनुमान लगाते हैं कि चतुर्भुज ABCD दो त्रिभुजों से बनता है,

यानी ADC और ABC।

चूँकि हम जानते हैं कि त्रिभुज के अंतः कोणों का योग 180° होता है,

कोणों की मापों का योग 180° + 180° = 360° . होता है

understanding quadrilaterals class 8 solutions pdf

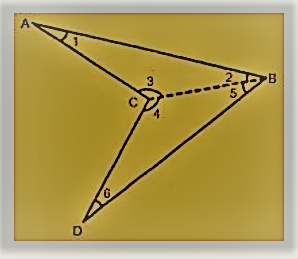
आइए हम एक अन्य चतुर्भुज ABCD लें जो उत्तल नहीं है।

BC को इस प्रकार मिलाइए कि वह ABCD को दो त्रिभुजों ΔABC और BCD में विभाजित कर दे। ABC में,

∠1 + ∠2 + ∠3 = 180° (त्रिभुज का कोण योग गुण)

BCD में,

4 + ∠5 + ∠6 = 180° (त्रिभुज का कोण योग गुण)

, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180° + 180°

1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°

A + ∠B + C + D = 360°

इस प्रकार, यदि चतुर्भुज उत्तल नहीं है तो यह गुण धारण करता है।

4. तालिका की जांच करें। (प्रत्येक आकृति को त्रिभुजों में विभाजित किया गया है और उससे निकाले गए कोणों का योग।)

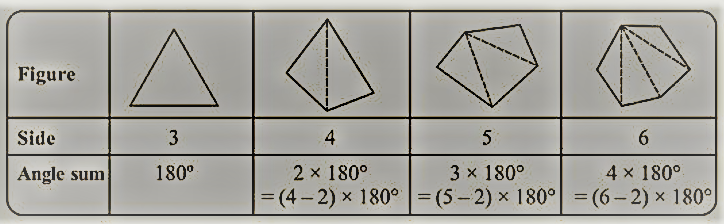ncert solutions for class 8 maths chapter 3 in hindi

भुजाओं की संख्या वाले उत्तल बहुभुज के कोणों के योग के बारे में आप क्या कह सकते हैं? (ए) 7 (बी) 8 (सी) 10 (डी) एन

समाधान:

n भुजा वाले बहुभुज का कोण योग = (n-2)×180°

ए) 7

यहाँ, n = 7

अत: कोणों का योग = (7-2)×180° = 5×180° = 900°

बी) 8

यहाँ, n = 8

अत: कोणों का योग = (8-2)×180° = 6×180° = 1080°

ग) 10

यहाँ, n = 10

अत: कोणों का योग = (10-2)×180° = 8×180° = 1440°

घ) नहीं

यहाँ, n = n

अत: कोणों का योग = (n-2)×180°

5. एक नियमित बहुभुज क्या है?

 

के एक नियमित बहुभुज का नाम बताइए

(i) 3 भुजाएँ (ii) 4 भुजाएँ (iii) 6 भुजाएँ हल:

नियमित बहुभुज: एक बहुभुज जिसकी भुजाएँ समान लंबाई और समान माप के कोण हों, सम बहुभुज कहलाता है। अर्थात्, एक सम बहुभुज समबाहु और समकोणिक दोनों होता है।

(i) तीन भुजाओं वाला एक सम बहुभुज समबाहु त्रिभुज कहलाता है।

(ii) 4 भुजाओं वाला एक सम बहुभुज वर्ग कहलाता है।

(iii) 6 भुजाओं वाला एक नियमित बहुभुज सम षट्भुज कहलाता है।

6. निम्नलिखित आकृतियों में कोण माप x ज्ञात कीजिए।

ncert solutions for class 8 maths chapter 3

समाधान:

a) आकृति में 4 भुजाएँ हैं। अत: यह एक चतुर्भुज है। चतुर्भुज के कोणों का योग = 360°

50° + 130° + 120° + x = 360°

300° + x = 360°

x = 360° – 300° = 60°

b) आकृति में 4 भुजाएँ हैं। अत: यह एक चतुर्भुज है। साथ ही, एक भुजा समकोण बनाते हुए लंबवत है।

चतुर्भुज के कोणों का योग = 360°

⇒ 90° + 70° + 60° + x = 360°

⇒ 220° + x = 360°

⇒ x = 360° - 220° = 140°

c) आकृति में 5 भुजाएँ हैं। अत: यह एक पंचभुज है।

ncert solutions for class 8 maths chapter 3 pdf

पंचभुज के कोणों का योग = 540° नीचे के दो कोण रैखिक युग्म होते हैं।

, 180° - 70° = 110°

180° - 60° = 120°

⇒ 30° + 110° + 120° + x + x = 540°

260° + 2x = 540°

⇒ 2x = 540° - 260° = 280°

⇒ 2x = 280°

= 140°

d) आकृति में 5 समान भुजाएँ हैं। अत: यह एक नियमित पंचभुज है। अत: इसके सभी कोण बराबर होते हैं।

5x = 540°

एक्स = 540°/5

⇒ एक्स = 108°

7.

understanding quadrilaterals class 8 solutions pdf

समाधान:

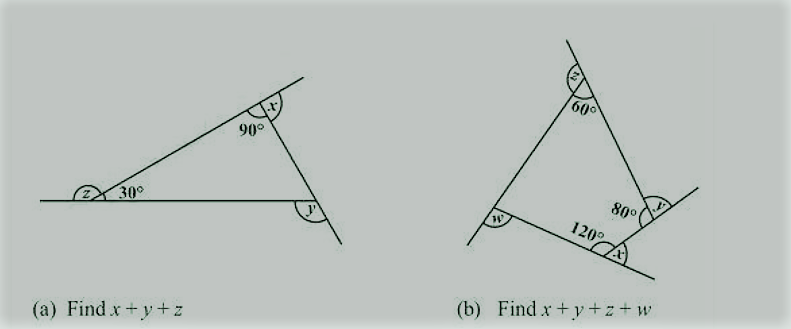
a) त्रिभुज के सभी कोणों का योग = 180°

त्रिभुज की एक भुजा = 180°- (90° + 30°) = 60°

x + 90° = 180° x = 180° - 90° = 90°

y + 60° = 180° y = 180° – 60° = 120°

z + 30° = 180° z = 180° - 30° = 150°

x + y + z = 90° + 120° + 150° = 360°

b) चतुर्भुज के सभी कोणों का योग = 360°

चतुर्भुज की एक भुजा = 360°- (60° + 80° + 120°) = 360° - 260° = 100°

x + 120° = 180° ⇒ x = 180° - 120° = 60°

y + 80° = 180° y = 180° - 80° = 100°

z + 60° = 180° z = 180° – 60° = 120°

डब्ल्यू + 100 डिग्री = 180 डिग्री ⇒ डब्ल्यू = 180 डिग्री - 100 डिग्री = 80 डिग्री

x + y + z + w = ​​60° + 100° + 120° + 80° = 360°

class 8 maths chapter 3 exercise 3.2 solution

1. निम्नलिखित आकृतियों में x ज्ञात कीजिए।

class 8 maths chapter 3 exercise 3.2 solution

समाधान:

ए)

class 8 maths chapter 3 exercise 3.2 solution

125° + m = 180° ⇒ m = 180° - 125° = 55° (रैखिक युग्म)

125° + n = 180° n = 180° - 125° = 55° (रैखिक जोड़ी)

x = m + n (किसी त्रिभुज का बाह्य कोण 2 सम्मुख अंत: 2 कोणों के योग के बराबर होता है)

x = 55° + 55° = 110°

बी)

ncert solutions for class 8 maths 

दो आंतरिक कोण समकोण हैं = 90°

70° + m = 180° ⇒ m = 180° - 70° = 110° (रैखिक जोड़ी)

60° + n = 180° n = 180° – 60° = 120° (रैखिक युग्म) आकृति की पाँच भुजाएँ हैं और यह एक पंचभुज है।

अत: पंचभुज के कोणों का योग = 540° 90° + 90° + 110° + 120° + y = 540°

410° + y = 540° ⇒ y = 540° - 410° = 130°

x + y = 180° (रैखिक जोड़ी)

x + 130° = 180°

⇒ x = 180° - 130° = 50°

2. एक सम बहुभुज के प्रत्येक बहिष्कोण का माप ज्ञात कीजिए

 

(i) 9 भुजाएँ (ii) 15 भुजाएँ हल:

n भुजा वाले एक नियमित बहुभुज के कोणों का योग = (n-2)×180°

(i) 9 भुजा वाले एक नियमित बहुभुज के कोणों का योग = (9-2)×180°= 7×180° = 1260°

प्रत्येक आंतरिक कोण=1260/9 = 140°

प्रत्येक बाह्य कोण = 180° - 140° = 40°

या,

प्रत्येक बहिष्कोण = बाह्य कोणों का योग/कोणों की संख्या = 360/9 = 40°

(ii) 15 भुजा वाले नियमित बहुभुज के कोणों का योग = (15-2)×180°

= 13×180° = 2340°

प्रत्येक आंतरिक कोण = 2340/15 = 156°

प्रत्येक बहिष्कोण = 180° - 156° = 24°

या,

प्रत्येक बहिष्कोण = बाह्य कोणों का योग/कोणों की संख्या = 360/15 = 24°

3. एक समबहुभुज की कितनी भुजाएँ होती हैं यदि एक बहिष्कोण का माप 24° है? समाधान:

 

प्रत्येक बहिष्कोण = बाह्य कोणों का योग/कोणों की संख्या

24°= 360/ भुजाओं की संख्या

भुजाओं की संख्या = 360/24 = 15

इस प्रकार, नियमित बहुभुज में 15 भुजाएँ होती हैं।

4. एक समबहुभुज की कितनी भुजाएँ होती हैं, यदि इसका प्रत्येक आंतरिक कोण 165° का हो? समाधान:

आंतरिक कोण = 165°

बाह्य कोण = 180° - 165° = 15°

भुजाओं की संख्या = बाह्य कोणों/बाह्य कोणों का योग

भुजाओं की संख्या = 360/15 = 24

इस प्रकार, सम बहुभुज में 24 भुजाएँ होती हैं।

5.

क) क्या प्रत्येक बाहरी कोण की माप 22° के साथ एक नियमित बहुभुज बनाना संभव है?

बी) क्या यह एक नियमित बहुभुज का एक आंतरिक कोण हो सकता है? क्यों?

समाधान:

क) बाह्य कोण = 22°

भुजाओं की संख्या = बाह्य कोणों का योग/बाह्य कोण

भुजाओं की संख्या = 360/22 = 16.36

नहीं, हमारे पास एक नियमित बहुभुज नहीं हो सकता जिसमें प्रत्येक बाहरी कोण 22° हो क्योंकि यह 360 का भाजक नहीं है।

b) आंतरिक कोण = 22°

बाह्य कोण = 180° - 22° = 158°

नहीं, हमारे पास एक नियमित बहुभुज नहीं हो सकता जिसमें प्रत्येक बाहरी कोण 158° हो क्योंकि यह 360 का भाजक नहीं है।

6.

क) एक नियमित बहुभुज के लिए संभव न्यूनतम आंतरिक कोण क्या है? क्यों?

बी) एक नियमित बहुभुज के लिए अधिकतम संभव बाहरी कोण क्या है?

समाधान:

a) समबाहु त्रिभुज एक नियमित बहुभुज है जिसमें 3 भुजाओं का न्यूनतम संभव न्यूनतम आंतरिक कोण होता है क्योंकि न्यूनतम भुजाओं वाले नियमित को कम से कम 3 भुजाओं के साथ बनाया जा सकता है। चूंकि, त्रिभुज के आंतरिक कोणों का योग = 180°

प्रत्येक आंतरिक कोण = 180/3 = 60°

बी) समबाहु त्रिभुज एक नियमित बहुभुज है जिसमें 3 भुजाएं अधिकतम बाहरी कोण होती हैं क्योंकि कम से कम भुजाओं वाले नियमित बहुभुज में अधिकतम बाहरी कोण संभव होता है। अधिकतम बाहरी संभव = 180 - 60° = 120°

ncert solutions for class 8 maths chapter 3 in Hindi : Exerise 3.3 page no .6

1. एक समांतर चतुर्भुज ABCD दिया है। इस्तेमाल की गई परिभाषा या संपत्ति के साथ प्रत्येक कथन को पूरा करें।

(i) AD = …… (ii) DCB = ……

(iii) OC = …… (iv) m DAB + m ∠CDA = ……

समाधान:

(i) AD = BC (एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं)

(ii) ∠DCB = DAB (एक समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं) (iii) OC = OA (एक समांतर चतुर्भुज के विकर्ण बराबर होते हैं)

(iv) m DAB + m ∠CDA = 180°

2. निम्नलिखित समांतर चतुर्भुजों पर विचार कीजिए। अज्ञात x, y, z . के मान ज्ञात कीजिए

ncert solutions for class 8 maths chapter 3 in hindi

समाधान:

(I)

understanding quadrilaterals class 8 solutions pdf

y = 100° (एक समांतर चतुर्भुज के विपरीत कोण)

x + 100° = 180° (एक समांतर चतुर्भुज के आसन्न कोण)

x = 180° – 100° = 80°

x = z = 80° (एक समांतर चतुर्भुज के विपरीत कोण)

, x = 80°, y = 100° और z = 80°

ncert solutions for class 8 maths

50° + x = 180° ⇒ x = 180° - 50° = 130° (एक समांतर चतुर्भुज के आसन्न कोण) x = y = 130° (एक समांतर चतुर्भुज के विपरीत कोण)

x = z = 130° (समान कोण)

(iii)

ncert solutions for class 8 maths chapter 3 pdf

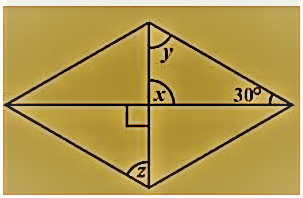
x = 90° (ऊर्ध्वाधर विपरीत कोण)

x + y + 30° = 180° (एक त्रिभुज का कोण योग गुण)

90° + y + 30° = 180°

y = 180° – 120° = 60°

साथ ही, y = z = 60° (वैकल्पिक कोण)

(iv)

ncert class 8 maths understanding quadrilaterals pdf

z = 80° (संबंधित कोण) z = y = 80° (वैकल्पिक कोण) x + y = 180° (आसन्न कोण)

x + 80° = 180° ⇒ x = 180° - 80° = 100°

(v)

ncert solutions for class 8 maths chapter 3

एक्स = 28o

y = 112o z = 28o

3. क्या एक चतुर्भुज ABCD एक समांतर चतुर्भुज हो सकता है यदि (i) D + B = 180°?

 

(ii) AB = DC = 8 सेमी, AD = 4 सेमी और BC = 4.4 सेमी?

(iii)∠A = 70° और ∠C = 65°?

समाधान:

(i) हाँ, एक चतुर्भुज ABCD एक समांतर चतुर्भुज है यदि D + B = 180° है, लेकिन यह भी होना चाहिए

कुछ शर्तों को पूरा किया जो हैं:

(ए) आसन्न कोणों का योग 180 डिग्री होना चाहिए।

(बी) विपरीत कोण बराबर होना चाहिए।

(ii) नहीं, विपरीत भुजाओं की लंबाई समान होनी चाहिए। यहाँ, AD BC

(iii) नहीं, सम्मुख कोण समान माप के होने चाहिए। ए सी

4. एक चतुर्भुज की एक खुरदरी आकृति खींचिए जो एक समांतर चतुर्भुज नहीं है, लेकिन इसके ठीक दो विपरीत कोण समान माप के हैं।

 

understanding quadrilaterals class 8 questions

समाधान:

ABCD एक चतुर्भुज की आकृति है जो एक समांतर चतुर्भुज नहीं है, लेकिन इसके ठीक दो विपरीत हैं

कोण जो B = D समान माप के हों। यह एक समांतर चतुर्भुज नहीं है क्योंकि ∠A C.

5. एक समांतर चतुर्भुज के दो आसन्न कोणों की माप 3 : 2 के अनुपात में है। समांतर चतुर्भुज के प्रत्येक कोण का माप ज्ञात कीजिए।

 

समाधान:

माना दो आसन्न कोणों A और ∠B के माप क्रमशः 3x और 2x हैं

समांतर चतुर्भुज ABCD।

A + B = 180°

⇒ 3x + 2x = 180°

5x = 180°

⇒ एक्स = 36°

हम जानते हैं कि समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।

A = ∠C = 3x = 3 × 36° = 108°

B = D = 2x = 2 × 36° = 72°

6. एक समांतर चतुर्भुज के दो आसन्न कोणों का माप बराबर होता है। समांतर चतुर्भुज के प्रत्येक कोण का माप ज्ञात कीजिए।

 

समाधान:

माना ABCD एक समांतर चतुर्भुज है।

समांतर चतुर्भुज के आसन्न कोणों का योग = 180°

A + B = 180°

2∠A = 180°

A = 90°

साथ ही, 90° + B = 180°

B = 180° – 90° = 90°

A = C = 90°

बी = डी = 90

°

7. आसन्न आकृति HOPE एक समांतर चतुर्भुज है। कोण का माप x, y और z ज्ञात कीजिए। उन गुणों का वर्णन करें जिनका उपयोग आप उन्हें खोजने के लिए करते हैं।

understanding quadrilaterals class 8 questions 7

 

समाधान:

y = 40° (वैकल्पिक आंतरिक कोण)

P = 70° (वैकल्पिक आंतरिक कोण)

∠P = H = 70° (एक समांतर चतुर्भुज के विपरीत कोण)

z = H - 40°= 70° – 40° = 30°

H + x = 180°

70° + x = 180°

⇒ x = 180° - 70° = 110°

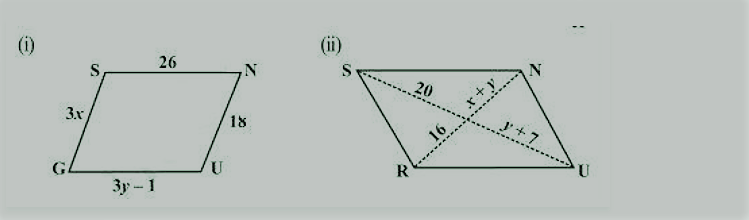
8. निम्नलिखित आकृतियाँ GUNS और RUNS समांतर चतुर्भुज हैं। एक्स और वाई खोजें। (लंबाई सेमी में हैं)

ncert solutions for class 8 maths chapter 3 exercise 3.3

समाधान:

(i) SG = NU और SN = GU (एक समांतर चतुर्भुज की विपरीत भुजाएँ बराबर होती हैं) 3x = 18

एक्स = 18/3

⇒ एक्स = 6

3y - 1 = 26 an

डी,

3y = 26 + 1

वाई = 27/3=9

एक्स = 6 और वाई = 9

(ii) 20 = y + 7 और 16 = x + y (एक समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं) y + 7 = 20

y = 20 - 7 = 13 और,

एक्स + वाई = 16

एक्स + 13 = 16

एक्स = 16 - 13 = 3

एक्स = 3 और वाई = 13

9. उपरोक्त आकृति में RISK और CLUE दोनों समांतर चतुर्भुज हैं। एक्स का मान ज्ञात करें।

ncert solutions for class 8 maths chapter 3 exercise 3.3

समाधान:

∠K + R = 180° (एक समांतर चतुर्भुज के आसन्न कोण संपूरक होते हैं)

⇒ 120° + R = 180°

R = 180° – 120° = 60°

साथ ही, R = SIL (संगत कोण)

एसआईएल = 60°

साथ ही, ∠ECR = ∠L = 70° (संगत कोण) x + 60° + 70° = 180° (एक त्रिभुज का कोण योग)

x + 130° = 180°

⇒ x = 180° - 130° = 50°

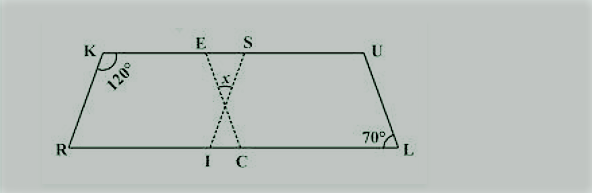
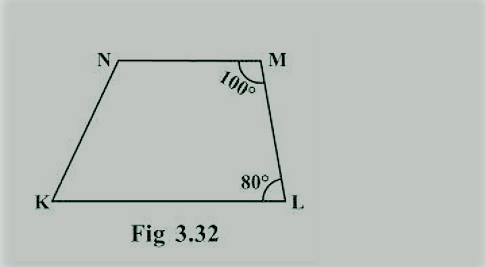
10. स्पष्ट कीजिए कि यह आकृति एक समलंब कैसे है। इसकी कौन सी दो भुजाएँ समानांतर हैं?

ncert solutions for class 8 maths chapter 3

समाधान:

जब एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि तिर्यक रेखा के एक ही तरफ आसन्न कोणों का योग 180° हो तो रेखाएँ एक दूसरे के समानांतर होती हैं। यहाँ, M + L = 100° + 80° = 180°

इस प्रकार, एमएन || लालकृष्ण

चूंकि चतुर्भुज KLMN में समानांतर रेखा का एक जोड़ा है इसलिए यह एक समलम्ब है। MN और LK समानांतर रेखाएँ हैं।

ncert solutions for class 8 maths chapter 3 IN HINDI

समाधान:

m∠C + m∠B = 180° (एक ही तिर्यक रेखा के कोण)

m∠C + 120° = 180°

m∠C = 180°- 120° = 60°

12. P और ∠S का माप ज्ञात कीजिए यदि SP || आरक्यू? चित्र 3.34 में। (यदि आप m∠R पाते हैं, तो क्या एक से अधिक हैं

 

ncert solutions for class 8 maths chapter 3

एम∠पी खोजने की विधि?)

समाधान:

P + Q = 180° (एक ही तिर्यक रेखा के कोण)

P + 130° = 180°

P = 180° – 130° = 50°

साथ ही, ∠R + ∠S = 180° (एक ही तिर्यक रेखा के कोण)

90° + ∠S = 180°

S = 180° - 90° = 90°

अत: ∠P = 50° और ∠S = 90°

हाँ, m∠P ज्ञात करने की एक से अधिक विधियाँ हैं।

PQRS एक चतुर्भुज है। सभी कोणों के मापों का योग 360° होता है।

चूँकि, हम ∠Q, R और S की माप जानते हैं।

Q = 130°, ∠R = 90° और ∠S = 90°

P + 130° + 90° + 90° = 360°

P + 310° = 360°

P = 360° - 310° = 50°

ncert solutions for class 8 maths chapter 3 exercise 3.4

1. बताएं कि सही है या गलत।

 

(ए) सभी आयत वर्ग हैं।

(बी) सभी समचतुर्भुज समांतर चतुर्भुज हैं।

(c) सभी वर्ग समचतुर्भुज हैं और आयत भी हैं।

(डी) सभी वर्ग समांतर चतुर्भुज नहीं हैं।

(e) सभी काइट्स समचतुर्भुज हैं।

(f) सभी समचतुर्भुज पतंग हैं।

(g) सभी समांतर चतुर्भुज समलंब हैं।

(h) सभी वर्ग समलंब हैं।

समाधान:

(ए) झूठा।

क्योंकि, सभी वर्ग आयत हैं लेकिन सभी आयत वर्गाकार नहीं हैं।

(बी) सच

(सी) सच

(डी) झूठा।

क्योंकि, सभी वर्ग समांतर चतुर्भुज होते हैं क्योंकि सम्मुख भुजाएँ समानांतर होती हैं और सम्मुख कोण बराबर होते हैं।

(ई) झूठा।

क्योंकि, उदाहरण के लिए, पतंग की भुजाओं की लंबाई समान लंबाई की नहीं होती है।

(च) सच

(जी) सच

(ज) सच

2. उन सभी चतुर्भुजों की पहचान करें जिनमें हैं।

 

(ए) समान लंबाई के चार पक्ष (बी) चार समकोण

समाधान:

(a) समचतुर्भुज और वर्ग की चारों भुजाएँ समान लंबाई की हैं।

(बी) वर्ग और आयत में चार समकोण होते हैं।

3. समझाइए कि एक वर्ग कैसा होता है।

 

(i) एक चतुर्भुज (ii) एक समांतर चतुर्भुज (iii) एक समचतुर्भुज (iv) एक आयत हल

(i) वर्ग एक चतुर्भुज है क्योंकि इसकी चार भुजाएँ हैं।

(ii) वर्ग एक समांतर चतुर्भुज है क्योंकि इसकी सम्मुख भुजाएँ समानांतर होती हैं और सम्मुख कोण बराबर होते हैं।

(iii) वर्ग एक समचतुर्भुज है क्योंकि चारों भुजाएँ समान लंबाई की हैं और विकर्ण समकोण पर समद्विभाजित करते हैं।

(iv) वर्ग एक आयत है क्योंकि वर्ग का प्रत्येक आंतरिक कोण 90° . है

4. उन चतुर्भुजों के नाम लिखिए जिनके विकर्ण हैं।

 

(i) एक दूसरे को समद्विभाजित करते हैं (ii) एक दूसरे के लंबवत समद्विभाजक हैं (iii) समान हैं हल

(i) समांतर चतुर्भुज, समचतुर्भुज, वर्ग और आयत

(ii) समचतुर्भुज और वर्ग

(iii) आयत और वर्ग

5. समझाइए कि एक आयत एक उत्तल चतुर्भुज क्यों है। समाधान

 

आयत एक उत्तल चतुर्भुज है क्योंकि इसके दोनों विकर्ण आयत के अंदर स्थित हैं।

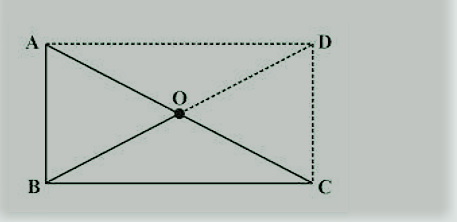
6. ABC एक समकोण त्रिभुज है और O समकोण के विपरीत भुजा का मध्य-बिंदु है। समझाइए कि O, A, B और C से समान दूरी पर क्यों है। (बिन्दुक वाली रेखाएँ आपकी सहायता के लिए अतिरिक्त रूप से खींची गई हैं)।

ncert solutions for class 8 maths chapter 3 in Hindi

समाधान

AD और DC इस प्रकार खींचे जाते हैं कि AD || बीसी और एबी || डीसी

एडी = बीसी और एबी = डीसी

ABCD एक आयत है क्योंकि सम्मुख भुजाएँ एक दूसरे के बराबर और समानांतर हैं और सभी

आंतरिक कोण 90° के हैं।

एक आयत में, विकर्ण समान लंबाई के होते हैं और एक दूसरे को समद्विभाजित भी करते हैं।

अत: AO = OC = BO = OD

इस प्रकार, O, A, B और C से समान दूरी पर है।