Download PDF For Factorisation class 8 notes in Hindi - class 8 math notes
factorisation class 8
Factors
एक व्यंजक को उसके गुणनखंडों के गुणनफल में गुणनखंडित किया जा सकता है। ये कारक बीजीय व्यंजक, चर और संख्याएँ भी हो सकते हैं।
Division of a monomial by another monomial
i) Division of 9x2 by 3:
9x2 ÷ 3 = 3(3x2) / 3 = 3x2
ii) Division of 6x2y by 2y:
6x2y÷2y = (6x2)y / 2y = 2y(3x2) / 2y = 3x2
Division of a polynomial by a monomial
एक बहुपद 2x3 + 4x2 + 6x is को एकपदी 2x से विभाजित किया जाता है जैसा कि नीचे दिखाया गया है:
(2x3+4x2+6x)2x = 2x3 / 2x + 4x22x + 6x / 2x = x2+ 2x + 3
factorisation class 8 : Division of a polynomial by a polynomial
एक बहुपद को एक बहुपद से विभाजित करने के लिए लंबी विभाजन विधि का उपयोग किया जाता है।
उदाहरण: 3x2 + 3x – 5 by (x – 1) का (x - 1) से भाग नीचे दिखाया गया है:
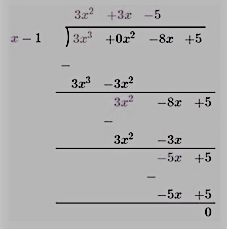 |
| factorisation class 8 |
Factors of natural numbers
प्रत्येक संख्या को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त किया जा सकता है। इसे प्राइम फैक्टर फॉर्म कहा जाता है।उदाहरण: 42 का अभाज्य गुणनखंड 2 x 3 x 7 है, जहां 2, 3 और 7 42 के गुणनखंड हैं।
factorisation class 8 : Algebraic expressions
एक बीजीय व्यंजक को गणितीय व्यंजक के रूप में परिभाषित किया जाता है जिसमें चर, संख्याएँ और संक्रियाएँ होती हैं। इस व्यंजक के मान स्थिर नहीं हैं। उदाहरण के लिए: x + 1, p - q, 3x, 2x+3y, 5a/6b आदि।Factors of algebraic expressions and factorisation
एक अपरिवर्तनीय कारक एक ऐसा कारक है जिसे कारकों के उत्पाद के रूप में आगे व्यक्त नहीं किया जा सकता है।बीजीय व्यंजकों को इरेड्यूसिबल रूप में व्यक्त किया जा सकता है।
factorisation class 8 notes : Factorisation by common factors
बीजीय व्यंजक को गुणनखंड करने के लिए, उच्चतम उभयनिष्ठ गुणनखंड निर्धारित किए जाते हैं।
उदाहरण: बीजीय व्यंजक -2y2 + 8y को 2y(-y+4) के रूप में लिखा जा सकता है, जहां 2y व्यंजक में सबसे अधिक उभयनिष्ठ गुणनखंड है।
Factorisation by regrouping terms
कुछ बीजीय व्यंजकों में यह संभव नहीं है कि प्रत्येक पद का एक उभयनिष्ठ गुणनखंड हो। इसलिए, उन बीजीय व्यंजकों का गुणनखंड करने के लिए, उभयनिष्ठ गुणनखंड वाले पदों को एक साथ समूहीकृत किया जाता है।
उदाहरण:
= 12a + n – na – 12
= 12a-12+n-na
= 12(a-1)-n(a-1)
= (12-n)(a-1)
(12-n) और (a-1) व्यंजक के गुणनखंड हैं 12a+n-na-12
factorisation class 8 : Method of Identities
Algebraic identities
बीजीय समीकरण जो चरों के सभी मानों के लिए सत्य होते हैं, बीजीय सर्वसमिकाएँ कहलाती हैं।कुछ पहचान हैं,
(a+b)2 = a2+ 2ab + b2
(a-b)2= a2– 2ab + b2
(a+b)(a-b)= a2 – b2
Factorisation using algebraic identities
गुणनखंडन के लिए बीजीय सर्वसमिकाओं का उपयोग किया जा सकता है
उदाहरण:
(i)9x2 + 12xy + 4y2
= ( 3x)2 + 2 x 3x x 2y+(2y)2
= (3x+4y)2
(ii)4a2 – b2 = (2a-b)(2a+b)
Visualisation of factorisation class 8
बीजीय व्यंजक x2 + 8x + 16 को (x+4)2 के रूप में लिखा जा सकता है। इसे नीचे दिखाए अनुसार देखा जा सकता है:


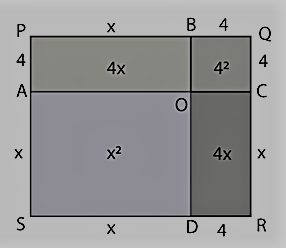








No comments:
Post a Comment