ncert solutions for class 9 maths chapter 7 in Hindi

ncert solutions for class 9 maths chapter 7 exercise 7.1

Ex 7.1 कक्षा 9 गणित प्रश्न 1.

चतुर्भुज ACBD में, AC = AD और AB A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि ABC ABD. आप BC और BD के बारे में क्या कह सकते हैं?

class 9 maths chapter 7 exercise 7.1 question 1

समाधान:

चतुर्भुज ACBD में, AC = AD और AB A का समद्विभाजक है।

अब, ∆ABC और ∆ABD में,

एसी = एडी (दिया गया)

सीएबी = डीएबी (एबी सीएबी को समद्विभाजित करता है)

और एबी = एबी (सामान्य)

∆ABC ≅ ∆ABD (एसएएस सर्वांगसमता अभिगृहीत द्वारा)

बीसी = बीडी (सीपीसीटी द्वारा)

Ex 7.1 कक्षा 9 गणित प्रश्न 2.

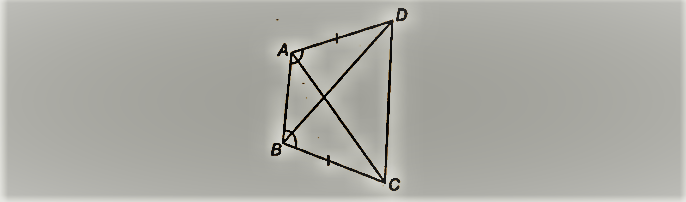
एबीसीडी एक चतुर्भुज है जिसमें एडी = बीसी और डीएबी = सीबीए (आकृति देखें)। साबित करो

ncert solutions for class 9 maths chapter 7 Ex 7.1 Q2

 (i) ∆ABD ≅ ∆BAC

(ii) बीडी = एसी

(iii) ∠ABD = ∠ बीएसी

समाधान:

चतुर्भुज ACBD में, हमारे पास AD = BC और ∠ DAB = ∠ CBA . है

(i) ∆ABC और ∆BAC में,

एडी = बीसी (दिया गया)

∠DAB = ∠CBA (दिया गया)

एबी = एबी (सामान्य)

ABD ≅ BAC (एसएएस सर्वांगसमता द्वारा)

(ii) चूँकि ∆ABD ≅ ∆BAC

बीडी = एसी [सी.पी.सी.टी. द्वारा]

(iii) चूँकि ∆ABD ≅ ∆BAC

 ∠ABD =  ∠BAC [C.P.C.T. द्वारा]

Ex 7.1 कक्षा 9 गणित प्रश्न 3.

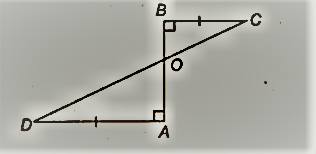
AD और BC एक रेखाखंड AB पर समान लंब हैं (देखिए आकृति)। दर्शाइए कि CD AB को समद्विभाजित करती है।

ncert solutions for class 9 maths chapter 7 EX Q.3

समाधान:

∆BOC और ∆AOD में, हमारे पास है

∠BOC = ∠AOD

ईसा पूर्व = एडी [दिया गया]

∠BOC = ∠AOD [ऊर्ध्वाधर सम्मुख कोण]

∴ ∆OBC ≅ ∆OAD [AAS सर्वांगसमता द्वारा]

ओबी = ओए [सी.पी.सी.टी. द्वारा]

अर्थात् O, AB का मध्य-बिंदु है।

अत: CD, AB को समद्विभाजित करती है।

Ex 7.1 कक्षा 9 गणित प्रश्न 4.

l और m दो समानांतर रेखाएँ हैं जो समानांतर रेखाओं p और q के एक अन्य युग्म द्वारा प्रतिच्छेदित होती हैं (देखिए आकृति)। दर्शाइए कि ABC = CDA है।

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.1 Q4

समाधान:

p || q and AC एक तिर्यक रेखा है,

∴ ∠BAC = ∠DCA …(1) [वैकल्पिक आंतरिक कोण]

इसके अलावा मैं || मी और एसी एक तिर्यक रेखा है,

∠BCA = ∠DAC …(2)

[वैकल्पिक आंतरिक कोण]

अब, ∆ABC और ∆CDA में, हमारे पास है

∠BAC = ∠DCA  [से (1)]

सीए = एसी [आम]

∠BCA = ∠DAC  [से (2)]

∆ABC ≅ ∆CDA [एएसए सर्वांगसमता द्वारा]

Ex 7.1 कक्षा 9 गणित प्रश्न 5.

रेखा l एक ∠ A का समद्विभाजक है और B, l पर कोई बिंदु है। BP और BQ, B से LA की भुजाओं पर लम्ब हैं (देखिए आकृति)। वो दिखाओ

(i)  ∆APB ≅ ∆AQB

(ii) BP = BQ या B भुजा A से समान दूरी पर है।

NCERT Solutions for Class 9 Maths Chapter 7 in Hindi

समाधान:

हमारे पास, ∠QAP का समद्विभाजक है।

∠QAB = ∠PAB

∠Q = ∠P [Each 90°]

∠ABQ = ∠ABP

[ए के कोण योग संपत्ति द्वारा]

अब, ∆APB और ∆AQB में, हमारे पास है

∠ABP = ∠ABQ [उपरोक्त सिद्ध]

एबी = बीए [सामान्य]

∠PAB = ∠QAB [दिया गया]

∆APB ≅ ∆AQB [एएसए सर्वांगसमता द्वारा]

चूँकि ∆APB ≅ ∆AQB

 BP = BQ [By C.P.C.T.]

, [एपी से बी की लंबवत दूरी]

= [AQ से B की लम्बवत दूरी]

इस प्रकार, बिंदु B,  ∠A की भुजाओं से समान दूरी पर है।

Ex 7.1 कक्षा 9 गणित प्रश्न 6.

आकृति में, AC = AE, AB = AD और ∠BAD =  ∠EAC। दर्शाइए कि BC = DE है।

triangles class 9 ncert solutions

समाधान:

हमारे पास है, ∠BAD = ∠EAC

DAC को दोनों पक्षों में जोड़ने पर, हमें प्राप्त होता है

∠BAD + ∠DAC = ∠EAC + ∠DAC

∠BAC = ∠DAE

अब, ∆ABC और ∆ADE में। अपने पास

∠BAC = ∠DAE [ऊपर प्रमाणित]

एबी = एडी [दिया गया]

एसी = एई [दिया गया]

∆ABC ≅ ∆ADE [एसएएस सर्वांगसमता द्वारा]

BC = DE [C.P.C.T. द्वारा]

Ex 7.1 कक्षा 9 गणित प्रश्न 7.

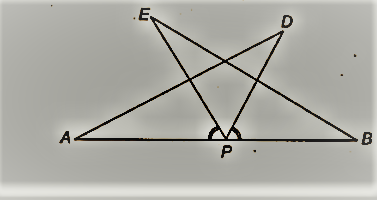
AS एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E AB के एक ही ओर स्थित बिंदु इस प्रकार हैं कि ∠ BAD = ∠ ABEऔर ∠ EPA = ∠ DPB। (रेखा - चित्र देखें)। वो दिखाओ

(i) ∆DAP ≅ ∆EBP

(ii) एडी = बीई

ncert solutions for class 9 maths chapter 7 PDF

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.1 Q7

समाधान:

हमारे पास, P, AB का मध्य-बिंदु है।

एपी = बीपी

∠EPA = ∠DPB [दिया गया]

दोनों पक्षों में EPD जोड़ने पर, हम प्राप्त करते हैं

∠EPA + ∠EPD = ∠DPB + ∠EPD

∠APD = ∠BPE

(i) अब,  ∆DAP और  ∆EBP में, हमारे पास है

∠PAD = ∠PBE [ ∵∠BAD = ∠ABE]

एपी = बीपी [ऊपर सिद्ध]

∠DPA = ∠EPB [ऊपर प्रमाणित]

DAP ≅ ∆EBP [एएसए सर्वांगसमता द्वारा]

(ii) चूँकि, ∆ DAP ≅ ∆ EBP

AD = BE [C.P.C.T. द्वारा]

Ex 7.1 कक्षा 9 गणित प्रश्न 8।

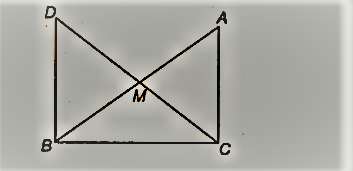
समकोण त्रिभुज ABC में, C पर समकोण, M कर्ण AB का मध्य-बिंदु है। C को M से जोड़ा जाता है और एक बिंदु D तक इस प्रकार बढ़ाया जाता है कि DM = CM हो। बिंदु D को बिंदु B से जोड़ा गया है (आकृति देखें)। वो दिखाओ

(i) ∆AMC ≅ ∆BMD

(ii) ∠DBC एक समकोण है

(iii) ∆DBC ≅ ∆ACB

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.1 Q8

(iv) CM = 12 AB

समाधान:

चूँकि M, AB का मध्य-बिंदु है।

BM = AM

(i) ∆AMC और ∆BMD में, हमारे पास है

सीएम = डीएम [दिया गया]

∠AMC = ∠BMD [ऊर्ध्वाधर सम्मुख कोण]

AM = BM [ऊपर प्रमाणित]

 ∆AMC ≅ ∆BMD [एसएएस सर्वांगसमता द्वारा]

(ii) चूँकि ∆AMC ≅ ∆BMD

∠MAC = ∠MBD [C.P.C.T. द्वारा]

लेकिन वे एकांतर आंतरिक कोणों का एक युग्म बनाते हैं।

∴ AC || DB

अब, BC एक तिर्यक रेखा है जो समानांतर रेखाओं AC और DB को प्रतिच्छेद करती है,

∠BCA + ∠DBC = 180° [सह-आंतरिक कोण]

परंतु ∠BCA = 90° [∆ABC, C पर समकोण है]

∴ 90° + ∠DBC = 180°

DBC = 90°

(iii) पुन:, ∆AMC ≅ ∆BMD[ऊपर प्रमाणित]

∴ एसी = बीडी [सी.पी.सी.टी. द्वारा]

अब, ∆DBC और ∆ACB में, हमारे पास है

बीडी = सीए [ऊपर प्रमाणित]

∠DBC = ∠ACB [प्रत्येक 90°]

बीसी = सीबी [सामान्य]

∆DBC ≅ ∆ACB  [एसएएस सर्वांगसमता द्वारा]

(iv) DBC ∆ACB . के रूप में

डीसी = एबी [सी.पी.सी.टी. द्वारा]

लेकिन डीएम = सीएम [दिया गया]

∴ सीएम = (1/2)DC = (1/2)AB

सीएम = (1/2)AB

NCERT Solutions for Class 9 Maths Chapter 7

Ex 7.2 कक्षा 9 गणित प्रश्न 1.

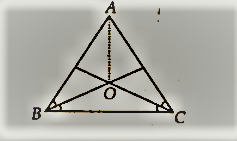
एक समद्विबाहु त्रिभुज ABC में, AB = AC के साथ, B और ∠C के समद्विभाजक एक दूसरे को 0 पर काटते हैं। A से 0 को मिलाइए। दर्शाइए कि

(i) ओबी = ओसी

(ii) AO ∠A . को समद्विभाजित करता है

समाधान:

i)  ∆ABC में, हमारे पास है

एबी = एसी [दिया गया]

∠ABC = ∠ACB  [A की समान भुजाओं के सम्मुख कोण बराबर होते हैं]

NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.2 Q1

12∠ABC = 12∠ACB

या OBC = OCB

OC = OB [एक के समान कोणों की सम्मुख भुजाएँ बराबर होती हैं]

(ii) ABO और ACO में, हमारे पास है

एबी = एसी [दिया गया]

∠OBA = ∠OCA [ ∵12∠B = 12∠C]

ओबी = ओसी [ऊपर सिद्ध]

∆ABO ≅ ∆ACO  [एसएएस सर्वांगसमता द्वारा]

∠OAB = ∠OAC [C.P.C.T. द्वारा]

AO, ∠A को समद्विभाजित करता है।

Ex 7.2 कक्षा 9 गणित प्रश्न 2.

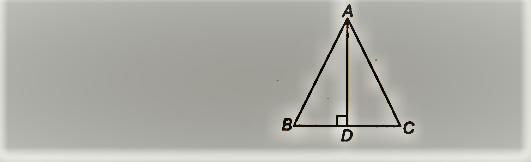
ABC में, AD BC का लम्ब समद्विभाजक है (देखिए आकृति)। दर्शाइए कि ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है।

NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.2 Q2

समाधान:

चूँकि AD, BC का समद्विभाजक है।

 BD = CD

अब, ∆ABD और ∆ACD में, हमारे पास है

AD = DA [सामान्य]

∠ADB = ∠ADC [प्रत्येक 90°]

बीडी = सीडी [ऊपर प्रमाणित]

 ∆ABD ≅  ∆ACD [एसएएस सर्वांगसमता द्वारा]

एबी = एसी [सी.पी.सी.टी. द्वारा]

अत: ∆ABC एक समद्विबाहु त्रिभुज है।

Ex 7.2 कक्षा 9 गणित प्रश्न 3.

ABC एक समद्विबाहु त्रिभुज है जिसमें समान भुजाओं AC और AB पर क्रमशः BE और CF के शीर्षलंब खींचे जाते हैं (देखिए आकृति)। दिखाएँ कि ये ऊँचाई बराबर हैं।

ncert solutions for class 9 maths chapter 7

समाधान:

∆ABC एक समद्विबाहु त्रिभुज है।

एबी = एसी

∠ACB = ∠ABC [A की समान भुजाओं के सम्मुख कोण बराबर होते हैं]

∠BCE = ∠CBF

अब, BEC और CFB . में

∠BCE = ∠CBF [उपरोक्त सिद्ध]

∠BEC = ∠CFB [प्रत्येक 90°]

बीसी = सीबी [सामान्य]

∆BEC ≅ ∆CFB  [AAS सर्वांगसमता द्वारा]

तो, बीई = सीएफ [सी.पी.सी.टी. द्वारा]

Ex 7.2 कक्षा 9 गणित प्रश्न 4।

ABC एक त्रिभुज है जिसमें AC और AB की भुजाओं के शीर्षलंब BE और CF बराबर हैं (देखिए आकृति)।

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.2 Q4

वो दिखाओ

(i) ∆ABE ≅ ∆ACF

(ii) AB = AC अर्थात ABC एक समद्विबाहु त्रिभुज है।

समाधान:

(i) ∆ABE और ∆ACE में, हमारे पास है

∠AEB = ∠AFC

[प्रत्येक 90° BE AC और CF ⊥ AB के रूप में]

∠A = ∠A [आम]

बीई = सीएफ [दिया गया]

ABE ≅ ∆ACF [AAS सर्वांगसमता द्वारा]

(ii) चूंकि,∆ABE ≅ ∆ACF

एबी = एसी [सी.पी.सी.टी. द्वारा]

ABC एक समद्विबाहु त्रिभुज है।

Ex 7.2 कक्षा 9 गणित प्रश्न 5.

ABC और DBC एक ही आधार BC पर समद्विबाहु त्रिभुज हैं (देखिए आकृति)। दर्शाइए कि ∠ ABD = ∠ACDहै।

triangles class 9 ncert solutions

समाधान:

ABC में, हमारे पास है

एबी = एसी [एबीसी एक समद्विबाहु त्रिभुज है]

∠ABC = ∠ACB …(1)

[एक की समान भुजाओं के सम्मुख कोण बराबर होते हैं]

पुनः, ∆BDC में, हमारे पास है

BD = CD [BDC एक समद्विबाहु त्रिभुज है]

∠CBD = ∠BCD …(2)

[A की समान भुजाओं के सम्मुख कोण बराबर होते हैं]

(1) और (2) को जोड़ने पर, हमारे पास है

∠ABC + ∠CBD = ∠ACB + ∠BCD

∠ABD = ∠ACD.

Ex 7.2 कक्षा 9 गणित प्रश्न 6.

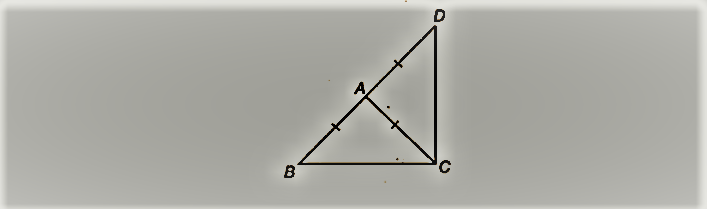
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। भुजा BA को D तक इस प्रकार बढ़ाया जाता है कि AD = AB हो (देखिए आकृति)। दर्शाइए कि  ∠BCD एक समकोण है।

NCERT Solutions for Class 9 Maths Chapter 7 Ex 7.2 Q6

समाधान:

AB = AC [Given] …(1) 

AB = AD [Given] …(2)

(1) और (2) से, हमारे पास है

एसी = एडी

अब,  ∆ABC में, हमारे पास है

∠ABC + ∠ACB + ∠BAC = 180° [A का कोण योग गुण]

⇒ 2∠ACB + ∠BAC = 180° …(3)

[∠ABC = ACB (A की समान भुजाओं के सम्मुख कोण बराबर होते हैं)]

इसी प्रकार, ∆ACD में,

∠ADC + ∠ACD + ∠CAD = 180°

2∠ACD + ∠CAD = 180° …(4)

[∠ADC = ACD (A की समान भुजाओं के सम्मुख कोण बराबर होते हैं)]

(3) और (4) को जोड़ने पर हमें प्राप्त होता है

2∠ACB + ∠BAC + 2 ∠ACD + ∠CAD = 180° + 180°

⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°

2∠BCD +180° = 360° [∠BAC और ∠CAD एक रैखिक युग्म बनाते हैं]

⇒ 2∠BCD = 360° - 180° = 180°

 ∠BCD = 180∘2 = 90°

अत: ∠BCD = 90°

Ex 7.2 कक्षा 9 गणित प्रश्न 7.

ABC एक समकोण त्रिभुज है जिसमें ∠A = 90° और AB = AC है, ∠B और ∠C ज्ञात कीजिए।

समाधान:

 ∆ABC में, हमारे पास AB = AC है [दिया है]

इनके सम्मुख कोण बराबर होते हैं।

NCERT Solutions for Class 9 Maths Chapter 7 Ex 7.2 Q7

∠ACB = ∠ABC

अब, ∠A + ∠B + ∠C = 180° [ a के कोणों का योग गुण]

90° + ∠B + ∠C = 180° [∠A = 90° (दिया गया)]

∠B + ∠C= 180°- 90° = 90°

लेकिन ∠B = ∠C

∠B = ∠C = 90∘2 = 45°

अत: ∠B = 45° और ∠C = 45°

Ex 7.2 कक्षा 9 गणित प्रश्न 8।

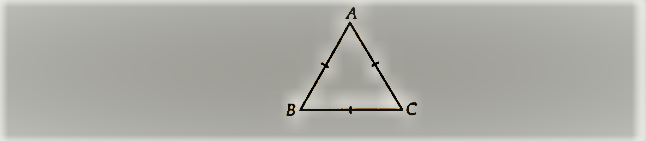
दर्शाइए कि एक समबाहु त्रिभुज के प्रत्येक कोण 60° के होते हैं।

समाधान:

ABC में, हमारे पास है

ncert solutions for class 9 maths chapter 7 pdf

AB = BC = CA

[एबीसी एक समबाहु त्रिभुज है]

AB = BC

∠A = ∠C …(1) [A की समान भुजाओं के सम्मुख कोण बराबर होते हैं]

इसी तरह, एसी = बीसी

∠A = ∠B …(2)

(1) और (2) से, हमारे पास है

∠A = ∠B = ∠C = x (मान लीजिए)

चूँकि, ∠A + ∠B + ∠C = 180° [A का कोण योग गुण]

एक्स + एक्स + एक्स = 180o

3x = 180°

एक्स = 60°

∠A = ∠B = ∠C = 60°

इस प्रकार, एक समबाहु त्रिभुज के प्रत्येक कोण 60° के होते हैं।

ncert solutions for class 9 maths chapter 7 exercise 7.3

Ex 7.3 कक्षा 9 गणित प्रश्न 1.

ABC और DBC एक ही आधार BC पर दो समद्विबाहु त्रिभुज हैं और शीर्ष A और D BC के एक ही तरफ हैं (आकृति देखें)। यदि AD को BC को P पर प्रतिच्छेद करने के लिए बढ़ाया जाता है, तो दर्शाइए कि

ncert solutions for class 9 maths chapter 7 exercise 7.3

(i) ∆ABD ≅ ∆ACD 

(ii) ∆ABP ≅ ∆ACP

(iii) AP ∠A और ∠D . को भी समद्विभाजित करता है

(iv) AP, BC का लम्ब समद्विभाजक है।

समाधान:

(i) ∆ABD और ∆ACD में, हमारे पास है

एबी = एसी [दिया गया]

एडी = डीए [सामान्य]

बीडी = सीडी [दिया गया]

∆ABD ≅ ∆ACD  [SSS सर्वांगसमता द्वारा]

∠BAD = ∠CAD [C.P.C.T. द्वारा] …(1)

(ii) ABP और ACP में, हमारे पास है

एबी = एसी [दिया गया]

∠BAP = ∠CAP  [से (1)]

एपी = पीए [सामान्य]

∆ABP ≅ ∆ACP [एसएएस सर्वांगसमता द्वारा]

(iii) चूँकि,∆ABP ≅ ∆ACP

∠BAP = ∠CAP [C.P.C.T. द्वारा]

AP, A का समद्विभाजक है।

पुनः, BDP और CDP में,

हमारे पास BD=CD है [दिया है]

डीपी = पीडी [सामान्य]

बीपी = सीपी [∵ ∆एबीपी ≅ ∆एसीपी]

⇒ A BDP = ACDP  [एसएसएस सर्वांगसमता द्वारा]

 ∠BDP = ∠CDP [C.P.C.T. द्वारा]

DP (या AP) BDC . का समद्विभाजक है

AP A और D का समद्विभाजक है।

(iv) जैसे,  ∆ABP ≅ ∆ACP

APS = APC, BP ​​= CP [C.P.C.T द्वारा]

परंतु APB + APC = 180° [रैखिक युग्म]

∴ ∠APB = ∠APC = 90°

AP ⊥ BC, also BP = CP

अत: AP, BC का लम्ब समद्विभाजक है।

Ex 7.3 कक्षा 9 गणित प्रश्न 2.

AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलंब है जिसमें AB = AC है। वो दिखाओ

(i) AD, BC को समद्विभाजित करता है

(ii) AD A . को समद्विभाजित करता है

समाधान:

(i) दायीं ओर ABD और ACD में, हमारे पास है

एबी = एसी [दिया गया]

ncert solutions for class 9 maths chapter 7 exercise 7.3

∠ADB = ∠ADC [Each 90°]

एडी = डीए [सामान्य]

∆ABD ≅ ∆∆ACD [RHS सर्वांगसमता द्वारा]

तो, बीडी = सीडी [सी.पी.सी.टी. द्वारा]

D, BC का मध्य-बिंदु है या AD, BC को समद्विभाजित करता है।

(ii) चूंकि, ABD ∆ACD,

BAD = CAD [C.P.C.T. द्वारा]

अत: AD, A . को समद्विभाजित करता है

Ex 7.3 कक्षा 9 गणित प्रश्न 3.

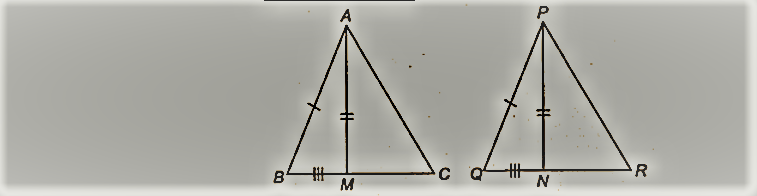
एक त्रिभुज ABC की दो भुजाएँ AB और BC और माध्यिका AM क्रमशः भुजाओं PQ और OR के बराबर हैं और PQR की माध्यिका PN है (देखिए आकृति)। वो दिखाओ

(i) ∆ABC ≅ ∆PQR
(ii) ∆ABM ≅ ∆PQN

ncert solutions for class 9 maths chapter 7 exercise 7.3 

समाधान:

∆ABC में, AM माध्यिका है।

BM = 1/2  BC ……(1)

∆PQR में, PN माध्यिका है।

∴ QN = 1/2QR …(2)

और BC = QR [दिया]

1/2BC = 1/2QR

BM = QN…(3) [(1) और (2) से]

(i) ABM और PQN में, हमारे पास है

AB = PQ , [दिया है]

AM = PN [दिया गया]

BM = QN [से (3)]

ABM ≅ ∆PQN [SSS सर्वांगसमता द्वारा]

(ii) चूँकि∆ABM ≅ ∆PQN

∠B = ∠Q …(4) [C.P.C.T. द्वारा]

अब, ABC और PQR में, हमारे पास है

∠B = ∠Q [से (4)]

AB = PQ [Given]

BC = QR [दिया गया]

∆ABC ≅ ∆PQR[एसएएस सर्वांगसमता द्वारा]

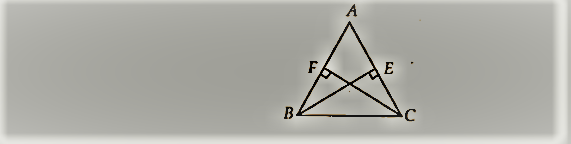
Ex 7.3 कक्षा 9 गणित प्रश्न 4।

BE और CF एक त्रिभुज ABC के दो समान शीर्षलंब हैं। RHS सर्वांगसमता नियम का प्रयोग करते हुए सिद्ध कीजिए कि त्रिभुज ABC समद्विबाहु है।

समाधान:

चूंकि BE ⊥ AC  [दिया गया है]

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.3 Q4

∴ BEC एक समकोण त्रिभुज है कि ∠BEC = 90°

इसी प्रकार, ∠CFB = 90°

अब, दायीं BEC और CFB में, हमारे पास है

बीई = सीएफ [दिया गया]

BC = CB [सामान्य कर्ण]

∠BEC = ∠CFB [प्रत्येक 90°]

∴ ∆BEC ≅ ∆CFB [RHS सर्वांगसमता द्वारा]

अतः, ∠BCE = ∠CBF [C.P.C.T. द्वारा]

या∠BCA =∠CBA

अब, ∆ABC में, ∠BCA = ∠CBA

AB = AC [एक के समान कोणों की सम्मुख भुजाएँ बराबर होती हैं]

ABC एक समद्विबाहु त्रिभुज है।

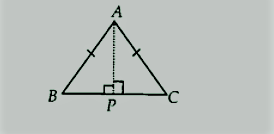
Ex 7.3 कक्षा 9 गणित प्रश्न 5.

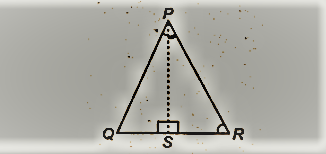
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP BC खींचकर दर्शाइए कि B = C है।

समाधान:

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.3 Q5

हमारे पास, AP ⊥ BC [दिया गया है]

∠APB = 90° और ∠APC = 90°

∆ABP और ∆ACP में, हमारे पास है

∠APB = ∠APC [प्रत्येक 90°]

एबी = एसी [दिया गया]

एपी = एपी [आम]

∴ ∆ABP ≅ ∆ACP [RHS सर्वांगसमता द्वारा]

तो, ∠B = ∠C [सी.पी.सी.टी. द्वारा]

ncert solutions for class 9 maths chapter 7 Ex 7.4

Ex 7.4 कक्षा 9 गणित प्रश्न 1.

दिखाएँ कि एक समकोण त्रिभुज में, कर्ण सबसे लंबी भुजा होती है।

समाधान:

आइए हम ∆ABC पर विचार करें कि ∠B = 90°

∴ ∠A + ∠B + ∠C = 180°

⇒ ∠A + 90°-+ ∠C = 180°

⇒ ∠A + ∠C = 90°

⇒∠A + ∠C = ∠B

∴ ∠B > ∠A तथा ∠B > ∠C

ncert solutions for class 9 maths chapter 7 ex 7.4

B की विपरीत भुजा A . की विपरीत भुजा से लंबी है

यानी, AC > BC।

इसी तरह, AC > AB

इसलिए, हम पाते हैं कि AC सबसे लंबी भुजा है। लेकिन AC त्रिभुज का कर्ण है। इस प्रकार, कर्ण सबसे लंबी भुजा है।

Ex 7.4 कक्षा 9 गणित प्रश्न 2.

आकृति में, ∆ABC की भुजाओं AB और AC को क्रमशः बिंदु P और Q तक बढ़ाया गया है। साथ ही, ∠PBC <∠QCB। दर्शाइए कि AC > AB।

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.4 Q2

समाधान:

∠ABC + ∠PBC = 180° [रैखिक युग्म]

और ∠ACB + ∠QCB = 180° [रैखिक युग्म]

परंतु ∠PBC < ∠QCB [दिया गया है] ⇒ 180° – ∠PBC > 180° – ∠QCB

AC > AB

ABC के विपरीत भुजा > ACB . के विपरीत भुजा

एसी> एबी।

Ex 7.4 कक्षा 9 गणित प्रश्न 3.

आकृति में, B <∠ A और ∠C <∠ D. दर्शाइए कि AD < BC है।

ncert solutions for class 9 maths chapter 7

हल: चूँकि ∠A > ∠B [दिया गया है]

∴ OB > OA …(1)

[बड़े कोण की सम्मुख भुजा लंबी होती है]

इसी तरह, OC > OD …(2)

(1) और (2) को जोड़ने पर, हमारे पास है

OB + OC > OA + OD

BC > AD

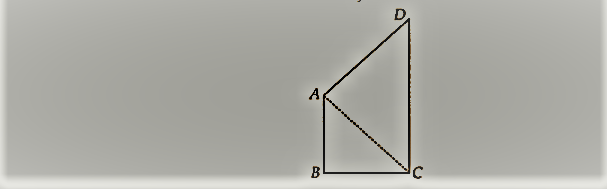
Ex 7.4 कक्षा 9 गणित प्रश्न 4।

AB और CD एक चतुर्भुज ABCD की क्रमशः सबसे छोटी और सबसे लंबी भुजाएँ हैं (देखिए आकृति)। दर्शाइए कि  ∠A >  ∠C तथा ∠B >∠D ।

ncert solutions for class 9 maths chapter 7

समाधान:

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.4 Q4

आइए AC ज्वाइन करें।

अब, ABC में, AB <BC [∵ AB चतुर्भुज ABCD की सबसे छोटी भुजा है] BC > AB

∠BAC > ∠BCA …(1)

[A की लंबी भुजा का सम्मुख कोण बड़ा होता है]

पुनः, ∆ACD, CD > AD . में

[CD चतुर्भुज ABCD की सबसे लंबी भुजा है]

∠CAD > ∠ACD …(2)

[∆ की लंबी भुजा का सम्मुख कोण बड़ा होता है]

(1) और (2) को जोड़ने पर, हमें प्राप्त होता है

∠BAC + ∠CAD > ∠BCA + ∠ACD

∠A> ∠C

इसी प्रकार, BD को मिलाने पर ∠B > ∠D. प्राप्त होता है।

Ex 7.4 कक्षा 9 गणित प्रश्न 5.

आकृति में, PR > PQ और PS  ∠QPR को समद्विभाजित करते हैं। सिद्ध कीजिए कि  ∠PSR >∠PSQ.

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.4 Q5

समाधान:

∆PQR में, PS ∠QPR को समद्विभाजित करता है [दिया है]

 ∠QPS =  ∠RPS

और  PR > PQ [दिया गया]

 ∠PQS >  ∠PRS [A की लंबी भुजा का सम्मुख कोण बड़ा होता है]

 ∠PQS + ∠QPS >  ∠PRS +  ∠RPS …(1) [∵∠QPS = ∠RPS]

∵ बाहरी ∠PSR = [∠PQS + ∠QPS]

और बाहरी ∠PSQ = [∠PRS + ∠RPS]

[एक बहिष्कोण अंतः सम्मुख कोणों के योग के बराबर होता है]

अब, (1) से, हमारे पास है

 ∠PSR =  ∠PSQ।

Ex 7.4 कक्षा 9 गणित प्रश्न 6.

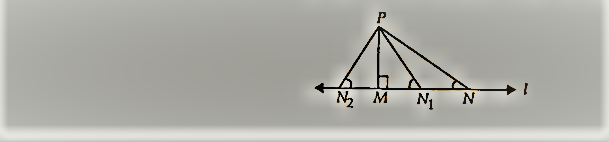
दिखाएँ कि किसी दिए गए बिंदु से खींचे गए सभी रेखाखंडों में से उस पर नहीं, लंबवत रेखा खंड सबसे छोटा है।

समाधान:

आइए हम ∆PMN पर विचार करें कि ∠M = 90°

ncert solutions for class 9 maths chapter 7 in Hindi

चूँकि, ∠M + ∠N+ ∠P = 180°

[एक त्रिभुज के कोणों का योग 180° होता है]

∠M = 90° [पीएम ⊥ l]

तो, ∠N + ∠P = M

∠N < ∠M

⇒ PM < PN …(1)

इसी तरह, PM < PN1 …(2)

और  PM < PN2 …(3)

(1), (2) और (3) से, हमें प्राप्त होता है कि PM रेखा I पर P से खींचा गया सबसे छोटा रेखाखंड है। इस प्रकार, लंब रेखा खंड एक रेखा पर उस बिंदु से खींची गई सबसे छोटी रेखा खंड है जो उस पर नहीं है।

NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.5

Ex 7.5 कक्षा 9 गणित प्रश्न 1.

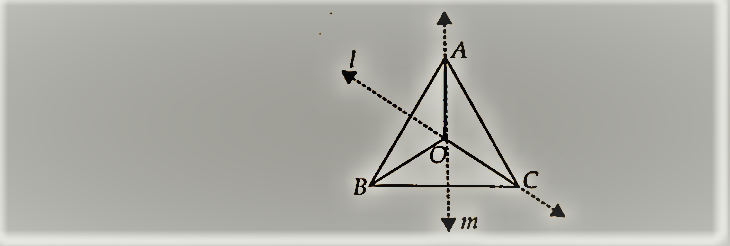
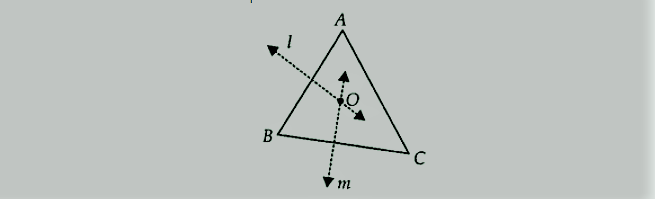
ABC एक त्रिभुज है। ABC के अभ्यंतर में एक बिंदु ज्ञात कीजिए जो ABC के सभी शीर्षों से समान दूरी पर है।

समाधान:

आइए एक ABC पर विचार करें।

AB का लंब समद्विभाजक l खींचिए।

BC का लम्ब समद्विभाजक m खींचिए।

माना दो लम्ब समद्विभाजक l और m, O पर मिलते हैं।

O अभीष्ट बिंदु है जो A, B और C से समान दूरी पर है।

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5 Q1

नोट: यदि हम केंद्र O और त्रिज्या OB या OC के साथ एक वृत्त खींचते हैं, तो यह A, B और C से होकर गुजरेगा। बिंदु O को त्रिभुज का परिकेन्द्र कहा जाता है।

Ex 7.5 कक्षा 9 गणित प्रश्न 2.

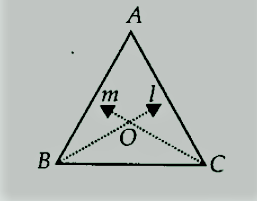
एक त्रिभुज में इसके अभ्यंतर में एक बिंदु खोजें जो त्रिभुज की सभी भुजाओं से समान दूरी पर हो।

समाधान:

आइए एक ∆ABC पर विचार करें।

 NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5 Q2

C का समद्विभाजक m खींचिए।

माना दो समद्विभाजक l और m, O पर मिलते हैं।

इस प्रकार, O अभीष्ट बिंदु है जो ∆ABC की भुजाओं से समान दूरी पर है।

नोट: यदि हम OM ⊥ BC खींचते हैं और O को केंद्र और OM को त्रिज्या लेकर एक वृत्त खींचते हैं, तो वृत्त त्रिभुज की भुजाओं को स्पर्श करेगा। बिंदु O को त्रिभुज का केंद्र बिंदु कहा जाता है।

ncert solutions for class 9 maths chapter 7

Ex 7.5 कक्षा 9 गणित प्रश्न 3.

एक विशाल पार्क में, लोग तीन बिंदुओं पर केंद्रित होते हैं (आकृति देखें)

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5 Q3

ए: जहां ये बच्चों के लिए अलग-अलग स्लाइड और झूले हैं।

B: जिसके पास एक मानव निर्मित झील स्थित है।

सी: जो एक बड़ी पार्किंग के पास है और मौजूद है।

आइसक्रीम पार्लर कहाँ स्थापित करना चाहिए? ताकि अधिकतम संख्या में व्यक्ति उससे संपर्क कर सकें?

[संकेत पार्लर ए, बी और सी से समान दूरी पर होना चाहिए।]

समाधान:

आइए हम A और B को मिलाते हैं और AB का लंब समद्विभाजक l खींचते हैं।

अब, B और C को मिलाइए और BC का लंब समद्विभाजक m खींचिए। माना लम्ब समद्विभाजक l और m, O पर मिलते हैं।

बिंदु O वह आवश्यक बिंदु है जहां आइसक्रीम पार्लर स्थापित किया जाना है।

नोट: यदि हम A और C को मिलाते हैं और लंब समद्विभाजक खींचते हैं, तो यह बिंदु O से भी मिलेगा (या गुजरेगा)।

 NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5 Q3.1

Ex 7.5 कक्षा 9 गणित प्रश्न 4.

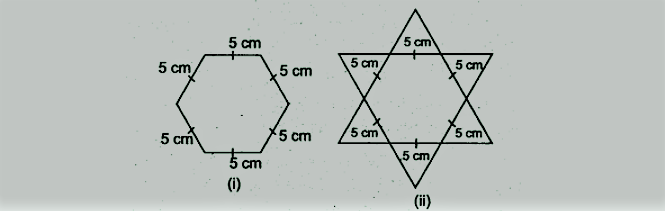
षट्कोणीय और तारे के आकार की रंगोली [देखिए आकृति (i) और (ii)] को यथासंभव 1 सेमी भुजा वाले समबाहु त्रिभुजों से भरकर पूरा कीजिए। प्रत्येक स्थिति में त्रिभुजों की संख्या गिनें। किसमें अधिक त्रिभुज हैं?

NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5 Q4

समाधान:

यह एक गतिविधि है।

हमें आकृति (i) में 1 सेमी भुजा वाले 150 समबाहु त्रिभुज और आकृति (ii) में 300 समबाहु त्रिभुजों की आवश्यकता है।

आकृति (ii) में अधिक त्रिभुज हैं।