NCERT solutions for class 9 maths in Hindi medium Chapter 2
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.1, NCERT Solutions for Class 9 Maths का हिस्सा हैं। यहां हमने एनसीईआरटी सोलूशन्स क्लास 9 गणित चैप्टर 2 बहुपद Ex 2.1 दिया है।
बहुआयामी पद
परिचय
एक चर में बहुपद
एक बहुपद के शून्यक
शेष प्रमेय
बहुपदों का गुणनखंड
बीजीय पहचान
सारांश
NCERT Solutions for Class 9 Maths Chapter 2
class 9th maths solutions for ex : 2.1
निम्नलिखित में से कौन से व्यंजक एक चर वाले बहुपद हैं और कौन से नहीं हैं? अपने उत्तर के कारण बताएं।
(i) 4x2 – 3x + 7
(ii) y2 + √2
(iii) 3 √t + t√2
(iv) y+
(v) x10+ y3+t50
समाधान:
(i) हमारे पास 4x2 – 3x + 7 = 4x2 – 3x + 7x0. है
यह एक चर में एक बहुपद है अर्थात x
क्योंकि x का प्रत्येक घातांक एक पूर्ण संख्या है।
(ii) हमारे पास y2 + √2 = y2 + √2y0 . है
यह एक चर में एक बहुपद है, अर्थात, y
क्योंकि y का प्रत्येक घातांक एक पूर्ण संख्या है।
(iii) हमारे पास 3 √t + t√2 = 3 √t1/2 + √2.t. है
यह बहुपद नहीं है, क्योंकि t का एक घातांक 12 है,
जो एक पूर्ण संख्या नहीं है।
(iv) हमारे पास yy +
यह बहुपद नहीं है, क्योंकि y का एक घातांक -1 है,
जो एक पूर्ण संख्या नहीं है।
(v) हमारे पास x10+ y3 + t50 . है
यहाँ, प्रत्येक चर का घातांक एक पूर्ण संख्या है, लेकिन x10 + y3 + t50 x, y और t में एक बहुपद है, अर्थात् तीन चरों में।
अत: यह एक चर वाला बहुपद नहीं है।
exercise 2.1 class 9 maths in hindi
निम्नलिखित में से प्रत्येक में x2 के गुणांक लिखिए
(i) 2 + x2 + x
(ii) 2 – x2 + x3
(iii)
(iv) √2 x – 1
समाधान:
(i) दिया गया बहुपद 2 + x2 + x. है।
x2 का गुणांक 1 है।
(ii) दिया गया बहुपद 2 – x2 + x3 है।
x2 का गुणांक -1 है।
(iii) दिया गया बहुपद
x2 का गुणांक π/2 है।
(iv) दिया गया बहुपद √2 x - 1 है।
x2 का गुणांक 0 है।
ncert solutions class 9 maths : Ex 2.1 कक्षा 9 गणित प्रश्न 3.
35 घात वाले द्विपद और 100 घात वाले एकपदी का एक-एक उदाहरण दीजिए।
समाधान:
(i) 35 डिग्री का पेट 3x35 -4हो सकता है।
(ii) 100 डिग्री का एकपदी √2y100 हो सकता है।
प्रश्न 4।
निम्नलिखित बहुपदों में से प्रत्येक की घात लिखिए।
(i) 5x3+4x2 + 7x
(ii) 4 – y2
(iii) 5t – √7
(iv) 3
समाधान:
(i) दिया गया बहुपद 5x3+4x2 + 7x है।
चर x की उच्चतम घात 3 है।
अत: बहुपद की घात 3 है।
(ii) दिया गया बहुपद 4 – y2 है। उच्चतम
चर y की शक्ति 2 है।
अत: बहुपद की घात 2 है।
(iii) दिया गया बहुपद 5t - 7 है। चर t की उच्चतम घात 1 है। अतः, बहुपद की घात 1 है।
(iv) चूंकि, 3 = 3x° [∵ x°=1]
अत: बहुपद की घात 0 है।
ncert class 9 maths : प्रश्न 5.
निम्नलिखित को रैखिक, द्विघात और घन बहुपद के रूप में वर्गीकृत करें।
(i) x2+ x
(ii) x – x3
(iii) y + y2+4
(iv) 1 + x
(v) 3t
(vi) r2
(vii) 7x3
समाधान:
(i) x2 + x की घात 2 है। अतः, यह एक द्विघात बहुपद है।
(ii) x – x3 की घात 3 है। अतः, यह एक घन बहुपद है।
(iii) y + y2 + 4 की घात 2 है। अतः, यह एक द्विघात बहुपद है।
(iv) 1 + x की घात 1 है। अतः यह एक रैखिक बहुपद है।
(v) 3t की घात 1 है। अतः, यह एक रैखिक बहुपद है।
(vi)r2 की घात 2 है। अतः, यह एक द्विघात बहुपद है।
(vii) 7x3 की घात 3 है। अतः, यह एक घन बहुपद है।
ncert solutions for class 9 maths chapter 2 exercise 2.2
प्रश्न 1।
बहुपद 5x – 4x2 + 3 का मान ज्ञात कीजिए
(i) एक्स = 0
(ii) एक्स = - 1
(iii) एक्स = 2
समाधान:
1et p(x) = 5x – 4x2 + 3
(i) p(0) = 5(0) - 4(0)2 + 3 = 0 - 0 + 3 = 3
अत: x = 0 पर 5x - 4x2 + 3 का मान 3 है।
(ii) p(-1) = 5(-1) - 4(-1)2 + 3
= - 5x - 4x2 + 3 = -9 + 3 = -6
अत: x = -1 पर 5x - 4x2 + 3 का मान -6 है।
(iii) p(2) = 5(2) - 4(2)2 + 3 = 10 - 4(4) + 3
= 10 - 16 + 3 = -3
अत: x = 2 पर 5x - 4x2 + 3 का मान - 3 है।
प्रश्न 2
निम्नलिखित बहुपदों में से प्रत्येक के लिए p(0), p(1) और p(2) ज्ञात कीजिए।
(i) p(y) = y2 - y + 1
(ii) p(t) = 2 + 1 + 2t2 - t3
(iii) पी(एक्स) = x3
(iv) p(x) = (x-1) (x+1)
समाधान:
(i) दिया गया है कि p(y) = y2 - y + 1।
∴ p(0) = (0)2 - 0 + 1 = 0 - 0 + 1 = 1
p(1) = (1)2 - 1 + 1 = 1 - 1 + 1 = 1
p(2) = (2)2 - 2 + 1 = 4 - 2 + 1 = 3
(ii) दिया गया है कि p(t) = 2 + t + 2t2 - t3
p(0) = 2 + 0 + 2(0)2 - (0)3
= 2 + 0 + 0 - 0=2
p(1) = 2 + 1 + 2(1)2 - (1)3
= 2 + 1 + 2 - 1 = 4
p(2) = 2 + 2 + 2(2)2 - (2)3
= 2 + 2 + 8 - 8 = 4
(iii) दिया गया है कि p(x) = x3
∴ p(0) = (0)3 = 0, पी(1) = (1)3 = 1
p(2) = (2)3 = 8
(iv) दिया गया है कि p(x) = (x - 1)(x + 1)
∴ p(0) = (0 - 1)(0 + 1) = (-1)(1) = -1
p(1) = (1 - 1)(1 +1) = (0)(2) = 0
p(2) = (2 - 1)(2 + 1) = (1)(3) = 3
प्रश्न 3।
सत्यापित करें कि क्या निम्नलिखित बहुपद के शून्यक हैं, उनके सामने इंगित किया गया है।
(i) p(x) = 3x + 1,x = -1/3
(ii) p(x) = 5x - , x = 4/5
(iii) p(x) = x2 – 1, x = x – 1
(iv) p(x) = (x + 1) (x - 2), x = - 1.2
(वी) पी (एक्स) = एक्स 2, एक्स = 0
(vi) p(x) = 1x + m, x = - m1
(vii) P(x) = 3x2 - 1, x = - 1/√3,2/√3
(viii) p(x) = 2x + 1, x = 12
समाधान:
(i) हमारे पास , p(x) = 3x + 1 . है
p[-(1/3)] = 3[-(1/3)] + 1 = -1 + 1 = 0
(ii) हमारे पास है, p(x) = 5x - π
p[-(1/3)] = 3[-(1/3)] + 1 = -1 + 1 = 0
(iii) हमारे पास है, p(x) = x2 - 1
∴ p(1) = (1)2 – 1 = 1 – 1=0
चूँकि, p(1) = 0, इसलिए x = 1 x2 -1 का एक शून्य है।
तो,p(-1) = (-1)2 -1 = 1 – 1 = 0
चूँकि p(-1) = 0, इसलिए, x = -1, भी x2 - 1 का एक शून्य है।
(iv) हमारे पास है, p(x) = (x + 1)(x - 2)
p(-1) = (-1 +1) (-1 – 2) = (0)(- 3) = 0
चूँकि, p(-1) = 0, इसलिए, x = -1, (x + 1)(x - 2) का एक शून्य है।
तो, p( 2) = (2 + 1)(2 – 2) = (3)(0) = 0
चूँकि, p(2) = 0, इसलिए, x = 2 भी (x + 1)(x - 2) का एक शून्य है।
(v) हमारे पास है, p(x) = x2
∴ p(o) = (0)2 = 0
चूँकि, p(0) = 0, इसलिए, x = 0, x2 का एक शून्यक है।
(vi) हमारे पास है, p(x) = lx + m
(vii) अपने पास p(x) = 3x2 – 1
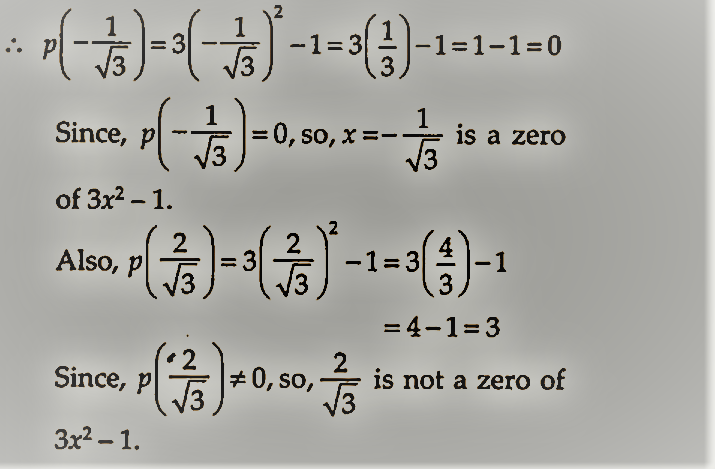 |
| ncert solutions for class 9 maths chapter 2 |
(viii) हमारे पास है, p(x) = 2x + 1
∴
चूँकि, p(12) 0, इसलिए, x = 12, 2x + 1 का शून्य नहीं है।
प्रश्न 4.
निम्नलिखित में से प्रत्येक स्थिति में बहुपद का शून्यक ज्ञात कीजिए
(i) p(x)=x+5
(ii) p(x)=x - 5
(iii) p(x) = 2x + 5
(iv) p(x) = 3x - 2
(वी) p(x) = 3x
(vi) p(x) = ax, a≠0
(vii) p(x) = cx + d, c ≠ 0 जहाँ c और d वास्तविक संख्याएँ हैं।
समाधान:
(i) हमारे पास p(x) = x + 5 है। चूँकि, p(x) = 0
x + 5 = 0
x = -5।
अत: x + 5 का शून्य -5 है।
(ii) हमारे पास, p(x) = x - 5 है।
चूँकि, p(x) = 0 x - 5 = 0 x = -5
अत: x - 5 का शून्यक 5 होता है।
(iii) हमारे पास p(x) = 2x + 5 है। चूँकि, p(x) = 0
⇒ 2x + 5 = 0
⇒ 2x = -5
⇒ x = −5/2
अत: 2x + 5 का शून्य −5/2 है।
(iv) हमारे पास p(x) = 3x - 2 है। चूंकि, p(x) = 0
3x - 2 = 0
3x = 2
एक्स = 23
अत: 3x - 2 का शून्य 2/3 . है
(v) हमारे पास, p(x) = 3x है। चूँकि, p(x) = 0
3x = 0 ⇒ x = 0
अत: 3x का शून्य 0 होता है।
(vi) हमारे पास, p(x) = ax, a 0 है।
चूँकि, p(x) = 0 => ax = 0 => x-0
इस प्रकार, कुल्हाड़ी का शून्य 0 है।
(vii) हमारे पास, p(x) = cx + d है। चूँकि, p(x) = 0
⇒ cx + d = 0 ⇒ cx = -d ⇒
अत: cx + d का शून्य −d/c . है
ncert solutions for class 9 maths chapter 2 ex 2.3
प्रश्न 1।
शेषफल ज्ञात कीजिए जब x3 + 3x2 + 3x + 1 को से विभाजित किया जाता है
(i) x + 1
(ii) x –
(iii) x
(iv) x + π
(v) 5 + 2x
समाधान:
मान लीजिए p(x) = x3 + 3x2 + 3x +1
(i) x + 1 का शून्यक -1 है।
∴ p(-1) = (-1)3 + 3(-1)2 + 3(-1) +1
= -1 + 3- 3 + 1 = 0
अत: अभीष्ट शेषफल = 0
(ii) x−1/2 का शून्यक 1/2 . है
ncert solutions for class 9 maths chapter 2 pdf
अत: अभीष्ट शेषफल = 278
(iii) x का शून्य 0 है।
∴ p(0) = (0)3 + 3(0)2 + 3(0) + 1
= 0 + 0 + 0 + 1 = 1
अत: अभीष्ट शेषफल = 1.
(iv) x + का शून्यक -π है।
p(-π) = (-π)3 + 3(- π)22 + 3(- π) +1
= -π3 + 3π2 + (-3π) + 1
= - 3 + 3π2 - 3π +1
अत: अभीष्ट शेषफल -π3 + 3π2 - 3π+1 है।
(v) 5 + 2x का शून्य −5/2 है।
ncert solutions for class 9 maths pdf
अत: अभीष्ट शेषफल -27/8 है।
प्रश्न 2
शेषफल ज्ञात कीजिए जब x3 – ax2 + 6x – a को x - a से विभाजित किया जाता है।
समाधान:
हमारे पास, p(x) = x3 – ax2 + 6x – a और x - a का शून्यक a है।
∴ p(a) = (a)3 – a(a)2 + 6(a) – a
= a3 – a3 + 6a – a = 5a
अत: अभीष्ट शेषफल 5a है।
प्रश्न 3।
जाँच कीजिए कि क्या 7 + 3x, 3x3+7x. का गुणनखंड है।
समाधान:
हमारे पास, p(x) = 3x3+7x है। और 7 + 3x का शून्य −7/3 है।
ncert solutions for class 9 maths chapter 2 hindi medium
चूंकि,( −490/9) ≠ 0
अर्थात। शेष 0 नहीं है।
3x3 + 7x, 7 + 3x से विभाज्य नहीं है।
इस प्रकार, 7 + 3x, 3x3 + 7x का गुणनखंड नहीं है।
ncert solutions for class 9 maths in Hindi medium : EX 2.4
प्रश्न 1।
निर्धारित करें कि निम्नलिखित में से किस बहुपद में (x +1) एक गुणनखंड है।
(i) x3+x2+x +1
(ii) x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 + 3x2 + x + 1
(iv) x3 – x2 – (2 +√2 )x + √2
समाधान:
x + 1 का शून्यक -1 होता है।
(i) मान लीजिए p(x) = x3 + x2 + x + 1
∴p(-1) = (-1)3 + (-1)2 + (-1) + 1 .
= -1 + 1 - 1 + 1
p(-1) = 0
तो, (x+ 1), x3 + x2 + x + 1.का एक गुणनखंड है।
(ii) मान लीजिए p(x) = x4 + x3 + x2 + x + 1
∴ P(-1) = (-1)4 + (-1)3 + (-1)2 + (-1)+1
= 1 - 1 + 1 - 1 + 1
⇒ पी(-1) 1
अतः, (x + 1) x4 + x3 + x2 + x+ 1. का गुणनखंड नहीं है।
(iii) माना p(x) = x4 + 3x3 + 3x2 + x + 1।
∴ p (-1)= (-1)4 + 3 (-1)3 + 3 (-1)2 + (- 1) + 1
= 1 – 3 + 3 – 1 + 1 = 1
⇒ p (-1) ≠ 0
अतः, (x + 1), x4 + 3x3 + 3x2 + x+ 1 का गुणनखंड नहीं है।
(iv) माना p (x) = x3 – x2 – (2 + √2) x + √2
∴ p (- 1) =(- 1)3- (-1)2 – (2 + √2)(-1) + √2
= -1 – 1 + 2 + √2 + √2
= 2√2
⇒ p (-1) ≠ 0
अतः, (x + 1), x3 – x2 – (2 + √2) x + √2.का गुणनखंड नहीं है।
प्रश्न 2
निम्नलिखित में से प्रत्येक मामले में g (x) p (x) का गुणनखंड है या नहीं, यह निर्धारित करने के लिए गुणनखंड प्रमेय का उपयोग करें
(i) p (x)= 2x3 + x2 – 2x – 1, g (x) = x + 1
(ii) p(x)= x3 + 3x2 + 3x + 1, g (x) = x + 2
(iii) p (x) = x3 – 4x2 + x + 6, g (x) = x – 3
समाधान:
(i) हमारे पास है, p (x)= 2x3 + x2 - 2x - 1 और g (x) = x + 1
∴ p(-1) = 2(-1)^3 + (-1)^2 - 2(-1) - 1
= 2(-1) + 1 + 2 - 1
= -2 + 1 + 2 -1 = 0
⇒ p(-1) = 0, इसलिए g(x) p(x) का एक गुणनखंड है।
(ii) हमारे पास p(x) x^3 + 3x^2 + 3x + 1 और g(x) = x + 2 है।
∴ p(-2) = (-2)^3 + 3(-2)^2 + 3(-2) + 1
= -8 + 12 - 6 + 1
= -14 + 13
= -1
⇒ p(-2) 0, इसलिए g(x) p(x) का गुणनखंड नहीं है।
(iii) हमारे पास, = x^3 - 4x^2 + x + 6 और g (x) = x - 3 . है
पी(3) = (3)^3 - 4(3)^2 + 3 + 6
= 27 - 4(9) + 3 + 6
= 27 - 36 + 3 + 6 = 0
⇒ p(3) = 0, इसलिए g(x) p(x) का एक गुणनखंड है।
प्रश्न 3।
k का मान ज्ञात कीजिए, यदि x - 1 निम्नलिखित में से प्रत्येक स्थिति में p (x) का गुणनखंड है
(i) p(x) = x^2 + x + k
(ii) p(x) = 2x^2 + kx + 2
(iii) p(x) = kx^2 - √2x + 1
(iv) p(x) = kx^2 - 3x + k
समाधान:
(x - 1) के लिए p(x) का गुणनखंड होने के लिए, p(1) 0 के बराबर होना चाहिए।
(i) यहाँ, p(x) = x^2 + x + k
चूँकि, p(1) = (1)2 +1 + k
p(1) = k + 2 = 0
k = -2।
(ii) यहाँ, p(x) = 2x^2 + kx + 2
चूँकि, p(1) = 2(1)^2 + k(1) + 2
= 2 + k + 2 = 0
के = -2 - √2 = - (2 + √2)
(iii) यहाँ, p(x) = kx^2 - 2x + 1
चूँकि, p(1) = k(1)^2 - (1) + 1
= के - 2 + 1 = 0
के = √2 -1
(iv) यहाँ, p(x) = kx^2 - 3x + k
p(1) = k(1)^2 - 3(1) + के
=k - 3 + k
= 2k - 3 = 0
k = 3/4
प्रश्न 4.
गुणनखंड
(i) 12x^2 - 7x+1
(ii) 2x^2 + 7x + 3
(iii) 6x^2 + 5x - 6
(iv) 3x^2 - x - 4
समाधान:
(i) हमारे पास है
12x^2 - 7x + 1 = 12x^2 - 4x - 3x + 1
= 4x (3x - 1) -1 (3x - 1)
= (3x -1) (4x -1)
अत: 12x^2 -7x + 3 = (2x - 1) (x + 3)
(ii) हमारे पास 2x^2 + 7x + 3 = 2x^2 + x + 6x + 3 . है
= x(2x + 1) + 3(2x + 1)
= (2x + 1)(x + 3)
इस प्रकार, 2×2 + 7x + 3 = (2x + 1)(x + 3)
(iii) हमारे पास 6x^2 + 5x - 6 = 6x^2 + 9x - 4x - 6 . है
= 3x(2x + 3) - 2(2x + 3)
= (2x + 3) (3x - 2)
अत: 6x^2 + 5x - 6 = (2x + 3) (3x - 2)
(iv) हमारे पास 3x^2 - x - 4 = 3x^2 - 4x + 3x - 4 . है
= x(3x - 4) + 1(3x - 4) = (3x - 4)(x + 1)
इस प्रकार, 3x^2 - x - 4 = (3x - 4)(x + 1)
प्रश्न 5.
गुणनखंड
(i) x^3 - 2x62 - x + 2
(ii) x^3 - 3x^2 - 9x - 5
(iii) x^3 + 13x^2 + 32x + 20
(iv) 2y^3 + y^2 - 2y - 1
समाधान:
(i) हमारे पास x^3 - 2x^2 - x + 2 . है
पदों को पुनर्व्यवस्थित करने पर, हमारे पास x^3 - x - 2x^2 + 2 . है
= x(x^2 - 1) - 2(x^2 - 1) = (x^2 - 1)(x - 2)
= [(x)^2 - (1)^2](x - 2)
= (x- 1)(x + 1)(x - 2)
[∵ (a^2 - b^2) = (a + b)(a-b)]
इस प्रकार, x^3 - 2x^2 - x + 2 = (x - 1)(x + 1)(x - 2)
(ii) हमारे पास x^3 - 3x^2 - 9x - 5 . है
= x^3 + x^2 - 4x^2 - 4x - 5x - 5,
= x^2 (x + 1) - 4x (x + 1) - 5 (x + 1)
= (x + 1)(x^2 - 4x - 5)
= (x + 1)(x^2 - 5x + x - 5)
= (x + 1) [x (x- 5) + 1 (x- 5)]
= (x + 1)(x - 5)(x + 1)
इस प्रकार, x^3 - 3x^2 - 9x - 5 = (x + 1)(x - 5)(x +1)
(iii) हमारे पास x^3 + 13x^2 + 32x + 20 . है
= x^3 + x^2 + 12x^2 + 12x + 20x + 20
= x^2(x + 1) + 12x(x + 1) + 20(x + 1)
= (x + 1)(x^2 + 12x + 20)
= (x + 1)(x^2 + 2x + 10x + 20)
= (x + 1) [x (x + 2) + 10 (x + 2)]
= (x + 1)(x + 2)(x + 10)
अत: x^3 + 13x^2 + 32x + 20
= (x + 1)(x + 2)(x + 10)
(iv) हमारे पास 2y^3 + y^2 - 2y - 1 . है
= 2y^3 - 2y^2 + 3y^2 - 3y + y - 1
= 2y^2(y-1) + 3y(y-1) + 1(y-1)
= (y -1) (2y^2 + 3y + 1)
= (y - 1)(2y^2 + 2y + y + 1)
= (y - 1)[2y(y + 1) + 1(y + 1)]
= (y - 1)(y + 1)(2y + 1)
अत: 2y3 + y2 - 2y - 1
= (y-1)(y+1)(2y+1)
ncert solutions for class 9 maths chapter 2 in Hindi :- Ex : 2.5
प्रश्न 1।
निम्नलिखित उत्पादों को खोजने के लिए उपयुक्त पहचान का प्रयोग करें
(i) (x + 4)(x + 10)
(ii) (x+8) (x-10)
(iii) (3x + 4) (3x - 5)
(iv) (y2+ 32) (y2- 32)
(v) (3 - 2x) (3 + 2x)
समाधान:
(i) हमारे पास है, (x+ 4) (x + 10)
पहचान का उपयोग करना
(x+ a) (x+ b) = x2 + (a + b) x+ ab।
हमारे पास है, (x + 4) (x + 10) = x2+(4 + 10) x + (4 x 10)
= x2 + 14x+40
(ii) हमारे पास है, (x+ 8) (x -10)
पहचान का उपयोग करना
(x + a) (x + b) = x2 + (a + b) x + ab
हमारे पास, (x + 8) (x - 10) = x2 + [8 + (-10)] x + (8) (- 10) है।
= x2 - 2x - 80
(iii) हमारे पास है, (3x + 4) (3x - 5)
पहचान का उपयोग करना
(x + a) (x + b) = x2 + (a + b) x + ab
(3x + 4) (3x - 5) = (3x) 2 + (4 - 5) x + (4) (- 5)
= 9x2 - x - 20
 |
| ncert solutions for class 9 maths chapter 2 : q.1 |
प्रश्न 2
सीधे गुणा किए बिना निम्नलिखित उत्पादों का मूल्यांकन करें
(i) 103*107
(ii) 95*96
(iii) 104*96
समाधान:
(i) हमारे पास 103 * 107 = (100 + 3) (100 + 7) है
= ( 100)2 + (3 + 7)(100)+ (3 x 7)
[(x + a)(x + b) = x2 + (a + b)x + ab का प्रयोग करके]
= 10000 + (10) x 100 + 21
= 10000 + 1000 + 21=11021
(ii) हमारे पास, 95 x 96 = (100 - 5) (100 - 4)
= ( 100)2+ [(- 5) + (- 4)] 100 + (- 5 x - 4)
[(x + a)(x + b) = x2 + (a + b)x + ab का प्रयोग करके]
= 10000 + (-9) + 20 = 9120
= 10000 + (-900) + 20 = 9120
(iii) हमारे पास 104 x 96 = (100 + 4) (100 - 4)
= (100)2-42
[(a + b)(a -b) = a2 - b2 का उपयोग करना]
= 10000 - 16 = 9984
प्रश्न 3।
उपयुक्त सर्वसमिकाओं का उपयोग करते हुए निम्नलिखित का गुणनखंड करें
(i) 9x^2 + 6xy + y2
(ii) 4y^2-4y + 1
(iii) x^2 - y2100
समाधान:
(i) हमारे पास 9x^2 + 6xy + y^2 . है
= (3x)^2 + 2(3x)(y) + (y)^2
= (3x + y)^2
[a^2 + 2ab + b^2 = (a + b)^2 का प्रयोग करके]
= (3x + y) (3x + y)
(ii) हमारे पास 4y2 - 4y + 12 . है
= (2y)^2 + 2(2y)(1) + (1)^2
= (2y-1)^2
[a^2 - 2ab + b^2 = (ab - b)^2 का प्रयोग करना]
= (2y - 1)(2y - 1)
प्रश्न 4.
उपयुक्त पहचान का उपयोग करके निम्नलिखित में से प्रत्येक का विस्तार करें
(i) (x+2y+ 4z)2
(ii) (2x – y + z)2
(iii) (- 2x + 3y + 2z)2
(iv) (3a -7b – c)z
(v) (- 2x + 5y – 3z)2
(vi) [
समाधान:
हम जानते हैं कि
(x + y + z)^2 = x^2 + y^2 + z^2 + 2xy + 2yz + 2zx
(i) (x + 2y + 4z)^2
= x^2 + (2y)^2 + (4z)^2 + 2(x)(2y) + 2(2y)(4z) + 2(4z)(x)
= x^2 + 4y^2 + 16z^2 + 4xy + 16yz + 8zx
(ii) (2x - y + z)^2 = (2x)^2 + (- y)^2 + z^2 + 2 (2x) (- y) + 2 (- y) (z) + 2 (z) (2x)
= 4x^2 + y^2 + z^2 - 4xy - 2yz + 4zx
(iii) (- 2x + 3y + 2z)^2 = (- 2x)^2 + (3y)^2 + (2z)^2 + 2 (- 2x) (3y) + 2 (3y) (2z) + 2 (2z) (- 2x)
= 4x^2 + 9y^2 + 4z^2 - 12xy + 12yz - 8zx
(iv) (3a -7b-c)^2 = (3a)^2 + (- 7b)^2 + (- c)^2 + 2 (3a) (- 7b) + 2 (- 7b) (- c) + 2 ( - c) (3 a)
= 9a^2 + 49b^2 + c^2 - 42ab + 14bc - 6ac
(v)(- 2x + 5y- 3z)^2 = (- 2x)^2 + (5y)^2 + (- 3z)^2 + 2 (- 2x) (5y) + 2 (5y) (- 3z) + 2 ( - 3z) (- 2x)
= 4x^2 + 25y^2 + 9z^2 - 20xy - 30yz + 12zx
NCERT Solutions for Class 9 Maths Chapter 2 बहुपद Ex 2.5 Q4
प्रश्न 5.
गुणनखंड
(i) 4x^2 + 9y^2 + 16z^2 + 12xy - 24yz - 16xz
(ii) 2x^2 + y^2 + 8z^2 - 2√2xy + 4√2yz - 8xz
समाधान:
(i) 4x^2 + 9y^2 + 16z^2 + 12xy - 24yz - 16xz
= (2x)^2 + (3y)^2 + (- 4z)^2 + 2 (2x) (3y) + 2 (3y) (- 4z) + 2 (- 4z) (2x)
= (2x + 3y - 4z)^ 2 = (2x + 3y + 4z) (2x + 3y - 4z)
(ii) 2x^2 + y^2 + 8z^2 - 2√2xy + 4√2yz - 8xz
= (- √2x)^2 + (y)^2 + (2 √2z)2y + 2(- √2x) (y)+ 2 (y) (2√2z) + 2 (2√2z) (- √2x )
= (- √2x + y + 2 √2z)^2
= (- 2x + y + 2 √2z) (- √2x + y + 2 √2z)
प्रश्न 6.
निम्नलिखित घनों को विस्तृत रूप में लिखिए
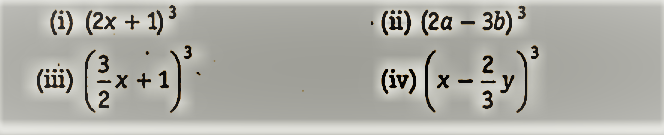 |
| NCERT Solutions for Class 9 Maths Chapter 2 |
समाधान:
हमारे पास, (x + y)^3 = x^3 + y^3 + 3xy(x + y) …(1)
और (x - y)^3 = x^3 - y^3 - 3xy(x - y) ...(2)
(i) (2x + 1)^3 = (2x)^3 + (1)^3 + 3(2x)(1)(2x + 1) [द्वारा (1)]
= 8x^3 + 1 + 6x (2x + 1)
= 8x^3 + 12x^2 + 6x + 1
(ii) (2a - 3b)^3 = (2a)^3 - (3b)^3 - 3(2a)(3b)(2a - 3b) [द्वारा (2)]
= 8a^3 - 27b^3 - 18ab (2a - 3b)
= 8a^3 - 27b^3 - 36a^2b + 54ab^2
 |
| ncert solutions for class 9 maths chapter 2 in hindi |
प्रश्न 7.
उपयुक्त सर्वसमिकाओं का प्रयोग करते हुए निम्नलिखित का मूल्यांकन कीजिए
(i) (99)^3
(ii) (102)^3
(iii) (998)^3
समाधान:
(i) हमारे पास, 99 = (100 -1)
99^3 = (100 - 1)^3
= (100) ^3 - 13 - 3 (100) (1) (100 -1)
[(a - b)^3 = a^3 - b^3 - 3ab (a - b) का प्रयोग करके]
= 1000000 - 1 - 300 (100 - 1)
= 1000000 -1 - 30000 + 300
= 1000300 - 30001 = 970299
(ii) हमारे पास 102 =100 + 2 . है
1023 = (100 + 2)^3
= (100)^3 + (2)^3 + 3(100)(2)(100 + 2)
[(a + b)^3 = a^3 + b^3 + 3ab (a + b) का प्रयोग करके]
= 1000000 + 8 + 600 (100 + 2)
= 1000000 + 8 + 60000 + 1200 = 1061208
(iii) हमारे पास 998 = 1000 - 2 . है
(998)^3 = (1000-2)^3
= (1000)^3 - (2)^3 - 3(1000)(2)(1000 - 2)
= 1000000000 - 8 - 6000 (1000 - 2)
= 1000000000 - 8 - 6000000 +12000
= 994011992
प्रश्न 8
निम्नलिखित में से प्रत्येक का गुणनखंड करें
(i) 8a^3 +b^3 + 12a^2b+6ab^2
(ii) 8a^3-b^3-12a^2b+6ab^2
(iii) 27-125a^3 -135a+225a^2
(iv) 64a^3 -27b^3 -144a^2b + 108ab^2
NCERT Solutions for Class 9 Maths Chapter 2 बहुपद Ex 2.5 Q8
समाधान:
(i) 8a^3 +b^3 +12a^2b+6ab^2
= (2a)^3 + (b)^3 + 6ab(2a + b)
= (2a)^3 + (b)^3 + 3(2a)(b)(2a + b)
= (2a + b)^3
[a3 + b3 + 3 ab(a + b) = (a + b)3 का प्रयोग करके]
= (2a + b)(2a + b)(2a + b)
(ii) 8a^3 - b^3 - 12a^2b + 6ab^2
= (2a)^3 - (b)^3 - 3(2a)(b)(2a - b)
= (2a - b)^3
= (2a - b) (2a - b) (2a - b)
(iii) 27 - 125a^3 - 135a + 225a^2
= (3)^3 - (5a)^3 - 3(3)(5a)(3 - 5a)
= (3 - 5a)^3
[a^3 + b^3 + 3 ab(a + b) = (a + b)^3 का प्रयोग करके]
= (3 - 5 a) (3 - 5 a) (3 - 5 a)
(iv) 64a^3 -27b^3 -144a^2b + 108ab^2
= (4a)^3 - (3b)^3 - 3(4a)(3b)(4a - 3b)
= (4a - 3b)^3
[a^3 – b^3 – 3 ab(a – b) = (a – b)^3 का प्रयोग करके]
= (4a – 3b)(4a – 3b)(4a – 3b)
NCERT Solutions for Class 9 Maths Chapter 2
प्रश्न 9
सत्यापित करें
(i) x3 + y3 = (x + y)-(x2 - xy + y2)
(ii) x3 - y3 = (x - y) (x2 + xy + y2)
समाधान:
(i) (x + y)3 = x3 + y3 + 3xy(x + y)
(x + y)3 - 3(x + y)(xy) = x3 + y3
(x + y)[(x + y)2-3xy] = x3 + y3
(x + y)(x2 + y2 - xy) = x3 + y3
इसलिए सत्यापित है।
(ii) ∵ (x - y)3 = x3 - y3 - 3xy(x - y)
(x - y)3 + 3xy(x - y) = x3 - y3
(x - y)[(x - y)2 + 3xy)] = x3 - y3
(x - y)(x2 + y2 + xy) = x3 - y3
इसलिए सत्यापित है।
प्रश्न 10.
निम्नलिखित में से प्रत्येक का गुणनखंड करें
(i) 27y3 + 125z3
(ii) 64m3 - 343n3
[संकेत प्रश्न 9 देखें]
समाधान:
(i) हम जानते हैं कि
x3 + y3 = (x + y) (x2 - xy + y2)
27y3 + 125z3 = (3y)3 + (5z)3
= (3y + 5z)[(3y)2 - (3y)(5z) + (5z)2]
= (3y + 5z)(9y2 - 15yz + 25z2)
(ii) हम जानते हैं कि
x3 - y3 = (x - y) (x2 + xy + y2)
64m3 - 343n3 = (4m)3 - (7n)3
= (4m - 7n)[(4m)2 + (4m)(7n) + (7n)2]
= (4m - 7n)(16m2 + 28mn + 49n2)
प्रश्न 11.
गुणनखंड 27x3 +y3 +z3 -9xyz।
समाधान:
अपने पास
27x3 + y3 + z3 - 9xyz = (3x)3 + (y)3 + (z)3 - 3(3x)(y)(z)
पहचान का उपयोग करना
x3 + y3 + z3 - 3xyz = (x + y + z) (x2 + y2 + z2 - xy - yz - zx)
हमारे पास है, (3x)3 + (y)3 + (z)3 - 3(3x)(y)(z)
= (3x + y + z)[(3x)3 + y3 + z3 - (3x × y) - (y × 2) - (z × 3x)]
= (3x + y + z) (9x2 + y2 + z2 - 3xy - yz - 3zx)
प्रश्न 12.
सत्यापित करो कि
x3 +y3 +z3 - 3xyz = 12 (x + y+z)[(x-y)2 + (y - z)2 +(z - x)2]
समाधान:
आर.एच.एस
R.H.S
=
=
=
=
= 2 x
= (x + y + z) (x2 + y2 + z2 - xy - yz - zx)
= x3 + y3 + z3 - 3xyz = L.H.S.
इसलिए सत्यापित है।
प्रश्न 13.
यदि x + y + z = 0, तो दर्शाइए कि x3 + y3 + z3 = 3 xyz।
समाधान:
चूँकि, x + y + z = 0
⇒ x + y = -z (x + y)3 = (-z)3
⇒ x3 + y3 + 3xy(x + y) = -z3
x3 + y3 + 3xy(-z) = -z3 [∵ x + y = -z]
⇒ x3 + y3 - 3xyz = -z3
x3 + y3 + z3 = 3xyz
अत: यदि x + y + z = 0, तो
x3 + y3 + z3 = 3xyz
प्रश्न 14.
वास्तव में घनों की गणना किए बिना, निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए
(i) (-12)3 + (7)3 + (5)3
(ii) (28)3 + (-15)3 + (-13)3
समाधान:
(i) हमारे पास है, (-12)3 + (7)3 + (5)3
माना x = -12, y = 7 और z = 5।
तब, x + y + z = -12 + 7 + 5 = 0
हम जानते हैं कि यदि x + y + z = 0, तो x3 + y3 + z3 = 3xyz
(-12)3 + (7)3 + (5)3 = 3[(-12)(7)(5)]
= 3[-420] = -1260
(ii) हमारे पास है, (28)3 + (-15)3 + (-13)3
मान लीजिए x = 28, y = -15 और z = -13।
तब, x + y + z = 28 - 15 - 13 = 0
हम जानते हैं कि यदि x + y + z = 0, तो x3 + y3 + z3 = 3xyz
(28)3 + (-15)3 + (-13)3 = 3(28)(-15)(-13)
= 3(5460) = 16380
प्रश्न 15.
निम्नलिखित आयतों में से प्रत्येक की लंबाई और चौड़ाई के लिए संभावित व्यंजक दें, जिनमें उनके क्षेत्रफल दिए गए हैं
(i) क्षेत्रफल 25a2 - 35a + 12
(ii) क्षेत्रफल 35y2 + 13y - 12
समाधान:
आयत का क्षेत्रफल = (लंबाई) x (चौड़ाई)
(i) 25a2 - 35a + 12 = 25a2 - 20a - 15a + 12 = 5a (5a - 4) - 3 (5a - 4) = (5a - 4) (5a - 3)
इस प्रकार, संभावित लंबाई और चौड़ाई (5a - 3) और (5a - 4) हैं।
(ii) 35y2 + 13y -12 = 35y2 + 28y - 15y -12
= 7y(5y + 4) - 3(5y + 4) = (5y + 4)(7y - 3)
इस प्रकार, संभावित लंबाई और चौड़ाई (7y - 3) और (5y + 4) हैं।
प्रश्न 16.
उन घनाभों की विमाओं के लिए संभावित व्यंजक क्या हैं जिनके आयतन नीचे दिए गए हैं?
(i) आयतन 3x2-12x
(ii) आयतन 12ky2 + 8ky - 20k
समाधान:
घनाभ का आयतन = (लंबाई) x (चौड़ाई) x (ऊंचाई)
(i) हमारे पास 3x2 - 12x = 3 (x2 - 4x) है।
= 3xxx (एक्स - 4)
घनाभ की संभावित विमाएँ 3, x और (x - 4) हैं।
(ii) हमारे पास 12ky2 + 8ky - 20k . है
= 4[3ky2 + 2ky - 5k] = 4[k(3y2 + 2y - 5)]
= 4 x k x (3y2 + 2y - 5)
= 4k [3y2 - 3y + 5y - 5]
= 4k [3y (y - 1) + 5 (y - 1)]
= 4k[(3y + 5) x (y - 1)]
= 4k x (3y + 5) x (y - 1)
इस प्रकार, घनाभ की संभावित विमाएँ 4k, (3y + 5) और (y -1) हैं।



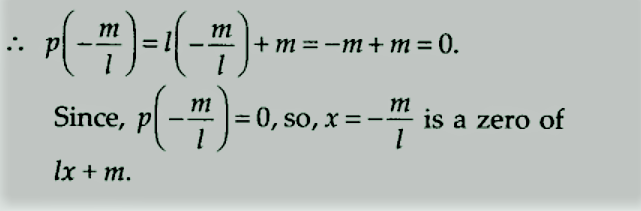


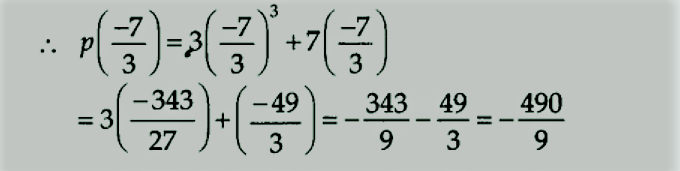

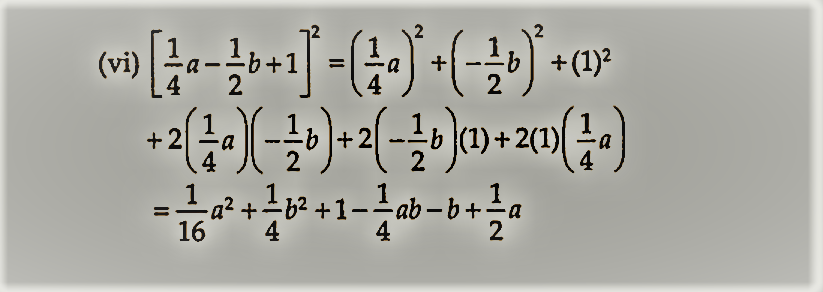
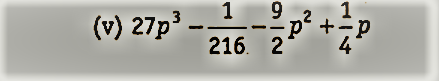









No comments:
Post a Comment