ncert solutions for class 9 maths chapter 1 number system
ncert solutions for class 9 maths chapter 1 number system एक विशेषज्ञ फैकल्टी द्वारा बनाए गए हैं। एनसीईआरटी गणित के ये समाधान छात्रों को पहले कार्यकाल के लिए समस्याओं को कुशलता और कुशलता से हल करने में मदद करते हैं। वे गणित के समाधान को इस तरह से तैयार करने पर भी ध्यान केंद्रित करते हैं कि छात्रों के लिए इसे समझना आसान हो। ncert solutions for class 9 maths chapter 1 का उद्देश्य छात्रों को इस अध्याय के अभ्यासों में दिए गए सभी प्रश्नों के उत्तरों के लिए विस्तृत और चरण-वार स्पष्टीकरण प्रदान करना है।
ncert solutions for class 9 maths chapter 1 pdf में, छात्रों को बहुत सारे महत्वपूर्ण विषयों से परिचित कराया जाता है, जो उन लोगों के लिए बहुत महत्वपूर्ण माने जाते हैं जो अपनी उच्च कक्षाओं में गणित को एक विषय के रूप में आगे बढ़ाना चाहते हैं। इन एनसीईआरटी समाधानों के आधार पर, छात्र अपनी आगामी प्रथम अवधि की परीक्षाओं के लिए अभ्यास कर सकते हैं और तैयारी कर सकते हैं, साथ ही कक्षा 10 की मूल बातों के साथ टर्म वार परीक्षा के लिए खुद को तैयार कर सकते हैं। एनसीईआरटी कक्षा 9 के ये मैथ्स सॉल्यूशंस मददगार हैं क्योंकि ये 2021-22 के सीबीएसई सिलेबस और इसके दिशानिर्देशों के नवीनतम अपडेट के संबंध में तैयार किए गए हैं।
ncert solutions for class 9 maths chapter 1 exercise 1.1
1. क्या शून्य एक परिमेय संख्या है? क्या आप इसे p/q के रूप में लिख सकते हैं जहाँ p और q पूर्णांक हैं और q 0?
समाधान:
हम जानते हैं कि, एक संख्या को परिमेय कहा जाता है यदि इसे p/q के रूप में लिखा जा सकता है, जहाँ p और q पूर्णांक हैं और q 0।
'0' का मामला लेते हुए,
शून्य को 0/1, 0/2, 0/3 ... के साथ-साथ 0/1, 0/2, 0/3 के रूप में भी लिखा जा सकता है।
चूँकि यह आवश्यक शर्त को पूरा करता है, हम यह निष्कर्ष निकाल सकते हैं कि 0 को p/q रूप में लिखा जा सकता है, जहाँ q या तो धनात्मक या ऋणात्मक संख्या हो सकती है।
अतः 0 एक परिमेय संख्या है।
2. 3 और 4 के बीच छह परिमेय संख्याएँ ज्ञात कीजिए।
समाधान:
3 और 4 के बीच अनंत परिमेय संख्याएँ हैं।
चूँकि हमें 3 और 4 के बीच 6 परिमेय संख्याएँ ज्ञात करनी हैं, हम 3 और 4 दोनों संख्याओं को 6+1 = 7 (या 6 से बड़ी कोई भी संख्या) से गुणा करेंगे।
यानी, 3 × (7/7) = 21/7
और, 4 × (7/7) = 28/7। 21/7 और 28/7 के बीच की संख्याएँ परिमेय होंगी और 3 और 4 के बीच होंगी।
अतः, 22/7, 23/7, 24/7, 25/7, 26/7, 27/7, 3 और 4 के बीच की 6 परिमेय संख्याएँ हैं।
3. 3/5 और 4/5 के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
समाधान:
3/5 और 4/5 के बीच अनंत परिमेय संख्याएँ हैं।
3/5 और 4/5 के बीच 5 परिमेय संख्याएँ ज्ञात करने के लिए, हम 3/5 और 4/5 दोनों संख्याओं को गुणा करेंगे
5+1=6 (या 5 से बड़ी कोई भी संख्या) के साथ
यानी, (3/5) × (6/6) = 18/30
और, (4/5) × (6/6) = 24/30
18/30 और 24/30 के बीच की संख्याएँ परिमेय होंगी और 3/5 और 4/5 के बीच होंगी।
इसलिए, 19/30, 20/30, 21/30, 22/30, 23/30 3/5 और 4/5 के बीच की 5 परिमेय संख्याएं हैं।
4. बताएं कि निम्नलिखित कथन सत्य हैं या गलत। अपने उत्तरों के लिए कारण दीजिए।
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
समाधान:
सत्य
प्राकृत संख्याएँ- 1 से अनंत तक की संख्याएँ (अंश या दशमलव के बिना)
अर्थात प्राकृत संख्याएँ = 1,2,3,4…
पूर्ण संख्याएँ - 0 से अनंत तक की संख्याएँ (अंश या दशमलव के बिना)
यानी, पूर्ण संख्याएँ = 0,1,2,3…
या, हम कह सकते हैं कि पूर्ण संख्याओं में प्राकृत संख्याओं के सभी अवयव और शून्य होते हैं।
प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है; हालाँकि, प्रत्येक पूर्ण संख्या एक प्राकृत संख्या नहीं होती है।
(ii) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।
समाधान:
असत्य
पूर्णांक- पूर्णांक संख्याओं का समूह होता है जिसमें धनात्मक, ऋणात्मक और 0 होते हैं; भिन्नात्मक और दशमलव संख्याओं को छोड़कर।
यानी, पूर्णांक = {…-4,-3,-2,-1,0,1,2,3,4…}
पूर्ण संख्याएँ - 0 से अनंत तक की संख्याएँ (अंश या दशमलव के बिना)
यानी, पूरी संख्या = 0,1,2,3…।
इसलिए, हम कह सकते हैं कि पूर्णांकों में पूर्ण संख्याएँ और ऋणात्मक संख्याएँ शामिल होती हैं।
प्रत्येक पूर्ण संख्या एक पूर्णांक है; हालांकि, प्रत्येक पूर्णांक एक पूर्ण संख्या नहीं है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
समाधान:
असत्य
परिमेय संख्याएँ- p/q के रूप में सभी संख्याएँ, जहाँ p और q पूर्णांक हैं और q≠0।
यानी परिमेय संख्याएं = 0, 19/30, 2, 9/-3, -12/7…
पूर्ण संख्याएँ - 0 से अनंत तक की संख्याएँ (अंश या दशमलव के बिना)
यानी, पूरी संख्या = 0,1,2,3…।
इसलिए, हम कह सकते हैं कि पूर्णांकों में पूर्ण संख्याएँ और ऋणात्मक संख्याएँ शामिल होती हैं।
प्रत्येक पूर्ण संख्याएँ परिमेय होती हैं, हालाँकि, प्रत्येक परिमेय संख्याएँ पूर्ण संख्याएँ नहीं होती हैं।
ncert solutions for class 9 maths chapter 1 exercise 1.2
1. बताएं कि निम्नलिखित कथन सही हैं या गलत। अपने उत्तरों का औचित्य सिद्ध कीजिए।
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
समाधान:
सत्य
अपरिमेय संख्याएँ - एक संख्या को अपरिमेय कहा जाता है, यदि इसे p/q में नहीं लिखा जा सकता है, जहाँ p और q पूर्णांक हैं और q 0।
यानी अपरिमेय संख्याएँ = , e, 3, 5+√2, 6.23146…. , 0.101001001000….
वास्तविक संख्याएँ - परिमेय और अपरिमेय दोनों संख्याओं के संग्रह को वास्तविक संख्याएँ कहते हैं।
यानी, वास्तविक संख्याएँ = √2, √5, , 0.102…
प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है, तथापि प्रत्येक वास्तविक संख्या अपरिमेय संख्या नहीं होती है।
(ii) संख्या रेखा पर प्रत्येक बिंदु m के रूप का होता है जहाँ m एक प्राकृत संख्या है।
समाधान:
असत्य
कथन असत्य है क्योंकि नियम के अनुसार ऋणात्मक संख्या को वर्गमूल के रूप में व्यक्त नहीं किया जा सकता है।
जैसे, √9 =3 एक प्राकृत संख्या है।
लेकिन 2 = 1.414 एक प्राकृत संख्या नहीं है।
इसी तरह, हम जानते हैं कि संख्या रेखा पर ऋणात्मक संख्याएँ होती हैं लेकिन जब हम ऋणात्मक संख्या का मूल लेते हैं तो यह एक प्राकृत संख्या नहीं बल्कि एक सम्मिश्र संख्या बन जाती है।
जैसे, -7 = 7i, जहां मैं = √-1
यह कथन कि संख्या रेखा का प्रत्येक बिंदु m के रूप का है, जहाँ m एक प्राकृत संख्या है, असत्य है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।
समाधान:
असत्य
कथन असत्य है, वास्तविक संख्याओं में अपरिमेय और परिमेय दोनों संख्याएँ शामिल हैं। अतः प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या नहीं हो सकती।
वास्तविक संख्याएँ - परिमेय और अपरिमेय दोनों संख्याओं के संग्रह को वास्तविक संख्याएँ कहते हैं।
यानी, वास्तविक संख्याएँ = √2, √5, , 0.102…
अपरिमेय संख्याएँ - एक संख्या को अपरिमेय कहा जाता है, यदि इसे p/q में नहीं लिखा जा सकता है, जहाँ p और q पूर्णांक हैं और q 0।
यानी अपरिमेय संख्याएँ = , e, 3, 5+√2, 6.23146…. , 0.101001001000….
प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है, तथापि प्रत्येक वास्तविक संख्या अपरिमेय नहीं होती है।
2. क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो उस संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
समाधान:
नहीं, सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय नहीं होते हैं।
उदाहरण के लिए,
√4 = 2 परिमेय है।
√9 = 3 परिमेय है।
इसलिए, धनात्मक पूर्णांक 4 और 9 के वर्गमूल अपरिमेय नहीं हैं। (क्रमशः 2 और 3)।
3. दर्शाइए कि संख्या रेखा पर 5 को किस प्रकार निरूपित किया जा सकता है।
समाधान:
चरण 1: मान लीजिए कि रेखा AB एक संख्या रेखा पर 2 इकाई की है।
चरण 2: B पर, 1 इकाई लंबाई की एक लंब रेखा BC खींचिए।
चरण 3: सीए में शामिल हों
चरण 4: अब, ABC एक समकोण त्रिभुज है। पाइथागोरस प्रमेय को लागू करना,
AB2+BC2 = CA2
22+12 = CA2 = 5
CA =√5 इस प्रकार, CA √5 इकाई लंबाई की एक रेखा है।
चरण 4: CA को त्रिज्या और A को केंद्र मानकर एक चाप खींचते हैं जो स्पर्श करता है
संख्या रेखा। वह बिंदु जिस पर संख्या रेखा प्रतिच्छेद करती है
चाप 0 से √5 की दूरी पर है क्योंकि यह वृत्त की त्रिज्या है
जिसका केंद्र ए.
इस प्रकार,√5 को संख्या रेखा पर निरूपित किया जाता है जैसा कि चित्र में दिखाया गया है।
 |
| ncert solutions for class 9 maths chapter 1 exercise 1.2 |
4. कक्षा की गतिविधि ('वर्गमूल सर्पिल' का निर्माण करना): कागज की एक बड़ी शीट लें और 'वर्गमूल सर्पिल' का निर्माण निम्न प्रकार से करें। बिंदु 0 से प्रारंभ करें और इकाई लंबाई का एक रेखाखंड OP1 बनाएं। OP1 पर इकाई लंबाई का एक रेखाखंड P1P2 लंब खींचिए (देखिए आकृति 1.9)। अब OP2 पर लम्ब एक रेखाखंड P2P3 खींचिए। फिर OP3 पर लंबवत एक रेखाखंड P3P4 खींचिए। चित्र 1.9 में जारी :
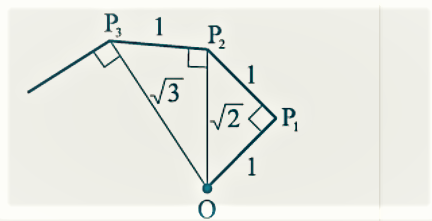 |
| class 9 maths ncert solutions |
इस तरह से निर्माण करते हुए, आप वर्गमूल सर्पिल द्वारा रेखा खंड Pn-1Pn प्राप्त कर सकते हैं, जो OPn-1 के लंबवत इकाई लंबाई का एक रेखा खंड खींचती है। इस तरह, आपने बिंदु P2, P3,…., Pn,… . बनाया होगा, और 2, √3, √4, … को दर्शाते हुए एक सुंदर सर्पिल बनाने के लिए उन्हें जोड़ दिया होगा।
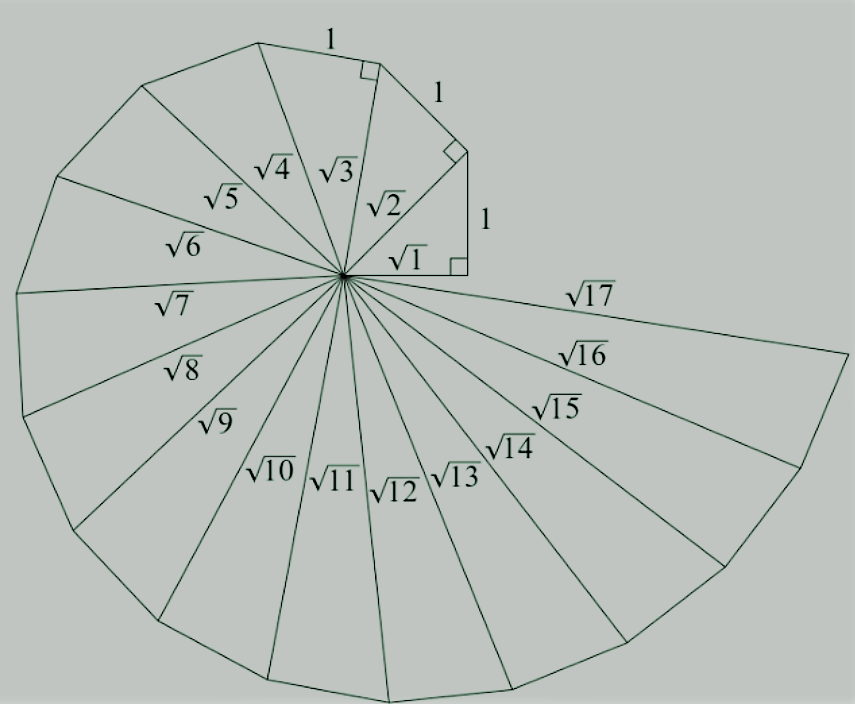 |
| ncert solutions for class 9 maths chapter 1 |
समाधान:
चरण 1: कागज पर एक बिंदु O अंकित करें। यहाँ, O वर्गमूल सर्पिल का केंद्र होगा।
चरण 2: 0 से क्षैतिज रूप से 1 सेमी की एक सीधी रेखा, OA खींचिए।
चरण 3: A से, 1 सेमी की एक लंब रेखा AB खींचिए।
चरण 4: ओबी से जुड़ें। यहाँ, OB 2 . का होगा
चरण 5: अब, B से, 1 सेमी की लंब रेखा खींचिए और अंत बिंदु C को चिह्नित कीजिए।
चरण 6: ओसी में शामिल हों। यहाँ, OC 3 . का होगा
चरण 7: 4, √5, 6… बनाने के लिए चरणों को दोहराएँ।
ncert solutions for class 9 maths chapter 1 exercise 1.3
1. निम्नलिखित को दशमलव रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है :
 |
| class 9 maths ncert solutions |
(i) 36/100
समाधान:
= 0.36 (समाप्त)
(ii) 1/11
समाधान:
 |
| ncert solutions for class 9 maths chapter 1 exercise 1.2 |
समाधान:
= 4.125 (समाप्त)
(iv) 3/13
समाधान:
 |
| ncert solutions for class 9 maths chapter 1 |
(वी) 2/11
समाधान:
 |
| ncert solutions for class 9 maths chapter 1 exercise 1.2 |
(vi) 329/400
समाधान:
 |
| class 9 maths ncert solutions in hindi |
2. आप जानते हैं कि 1/7 = 0.142857. क्या आप अनुमान लगा सकते हैं कि 2/7, 3/7, 4/7, 5/7, 6/7 के दशमलव प्रसार वास्तव में लंबा विभाजन किए बिना क्या हैं? यदि हां, तो कैसे?
[संकेत: 1/7 का मान ज्ञात करते हुए शेषफलों का ध्यानपूर्वक अध्ययन करें।
समाधान:
 |
| ncert math solution class 9 |
3. निम्नलिखित को p/q के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं और q 0 है।
 |
| ncert math solution |
मान लें कि x = 0.666…
फिर, 10x = 6.666…
10x = 6 + x
9x = 6
एक्स = 2/3
समाधान:
= (4/10)+(0.777/10)
मान लें कि x = 0.777…
फिर, 10x = 7.777…
10x = 7 + x
एक्स = 7/9
(4/10)+(0.777../10) = (4/10)+(7/90) ( x = 7/9 और x = 0.777…0.777…/10 = 7/(9×10) = 7 /90 )
= (36/90)+(7/90) = 43/90
 |
| class 9 maths ncert solutions |
मान लें कि x = 0.001001…
फिर, 1000x = 1.001001…
1000x = 1 + x
999x = 1
एक्स = 1/999
4. एक्सप्रेस 0.999999…. पी/क्यू के रूप में। क्या आप अपने जवाब से हैरान हैं? अपने शिक्षक और सहपाठियों के साथ चर्चा करें कि उत्तर क्यों समझ में आता है।
समाधान:
मान लें कि x = 0.9999…..Eq (a)
दोनों पक्षों को 10 से गुणा करने पर,
10x = 9.9999…. समीकरण (बी)
समीकरण (बी) - समीकरण (ए), हम प्राप्त करते हैं
10x = 9.9999
-एक्स = -0.9999…
9x = 9
एक्स = 1
1 और 0.999999 के बीच का अंतर 0.000001 है जो नगण्य है।
इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि, 0.999 1 के पास बहुत अधिक है, इसलिए, 1 उत्तर को उचित ठहराया जा सकता है।
5. 1/17 के दशमलव प्रसार में अंकों के दोहराव वाले ब्लॉक में अंकों की अधिकतम संख्या कितनी हो सकती है? अपने उत्तर की जांच के लिए भाग का प्रदर्शन करें।
समाधान:
1/17
1 को 17 से भाग देना:
 |
| ncert solutions for class 9 maths chapter 1 number system |
1/17 के दशमलव प्रसार के दोहराव वाले ब्लॉक में 16 अंक होते हैं।
6. परिमेय संख्याओं के कई उदाहरणों को p/q (q 0) के रूप में देखें, जहां p और q पूर्णांक हैं जिनमें 1 के अलावा कोई सामान्य गुणनखंड नहीं है और जिनका दशमलव निरूपण (विस्तार) है। क्या आप अनुमान लगा सकते हैं कि q को कौन-सी संपत्ति संतुष्ट करनी चाहिए?
समाधान:
हम देखते हैं कि जब q 2, 4, 5, 8, 10… है तो दशमलव प्रसार सांत होता है। उदाहरण के लिए:
1/2 = 0. 5, हर q = 21
7/8 = 0. 875, हर q =23
4/5 = 0. 8, हर q = 51
हम देख सकते हैं कि सांत दशमलव उस स्थिति में प्राप्त किया जा सकता है जहां दी गई भिन्नों के हर के अभाज्य गुणनखंड में केवल 2 या केवल 5 या दोनों की घात होती है।
7. ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनावर्ती अनावर्ती हैं।
समाधान:
हम जानते हैं कि सभी अपरिमेय संख्याएँ अनावर्ती अनावर्ती होती हैं। दशमलव प्रसार वाली तीन संख्याएँ जो अनावर्ती अनावर्ती हैं, वे हैं:
√3 = 1.732050807568
√26 =5.099019513592
√101 = 10.04987562112
8. परिमेय संख्याओं 5/7 और 9/11 के बीच तीन भिन्न अपरिमेय संख्याएँ ज्ञात कीजिए।
समाधान:
 |
| class 9 maths ncert solutions |
तीन अलग-अलग अपरिमेय संख्याएँ हैं:
0.7307300700070007000073…
0.7507500700070007000075…
0.76076007600070007600076…
9. निम्नलिखित संख्याओं को उनके प्रकार के अनुसार परिमेय या अपरिमेय के रूप में वर्गीकृत करें:
(मैं) √23
समाधान:
√23 = 4.79583152331…
चूँकि संख्या असांत अनावर्ती है इसलिए यह एक अपरिमेय संख्या है।
(ii)√225
समाधान:
225 = 15 = 15/1
चूँकि संख्या को p/q रूप में दर्शाया जा सकता है, यह एक परिमेय संख्या है।
(iii) 0.3796
समाधान:
चूँकि संख्या, 0.3796, सांत है, यह एक परिमेय संख्या है।
(iv) 7.478478
समाधान:
संख्या, 7.478478, असांत है लेकिन आवर्ती है, यह एक परिमेय संख्या है।
(v) 1.10100100100001…
समाधान:
चूँकि संख्या, 1.10100100100001…, गैर-समाप्ति गैर-दोहराव (गैर-आवर्ती) है, यह एक अपरिमेय संख्या है।
ncert solutions for class 9 maths chapter 1 exercise 1.4
1. क्रमागत आवर्धन का प्रयोग करते हुए संख्या रेखा पर 3.765 की कल्पना कीजिए।
समाधान:
 |
| ncert solutions for class 9 maths chapter 1 exercise 1.4 |
 |
| ncert solutions for class 9 maths chapter 1 |
ncert solutions for class 9 maths chapter 1 exercise 1.5
1. निम्नलिखित संख्याओं को परिमेय या अपरिमेय के रूप में वर्गीकृत कीजिए:
(i) 2 -√5
समाधान:
हम जानते हैं कि, 5 = 2.2360679…
यहाँ, 2.2360679… अनावर्ती और अनावर्ती है।
अब, 5 के मान को 2 –√5 में प्रतिस्थापित करने पर, हम प्राप्त करते हैं,
2-√5 = 2-2.2360679… = -0.2360679
चूँकि संख्या, – 0.2360679…, अनावर्ती अनावर्ती है, 2 –√5 एक अपरिमेय संख्या है।
(ii) (3 +√23)- √23
समाधान:
(3 +√23) –√23 = 3+√23–√23
= 3
= 3/1
चूँकि संख्या 3/1 p/q रूप में है, (3 +√23)- √23 परिमेय है।
(iii) 2√7/7√7
समाधान:
2√7/7√7 = ( 2/7)× (√7/√7)
हम जानते हैं कि (√7/√7) = 1
इसलिए, ( 2/7)× (√7/√7) = (2/7)×1 = 2/7
चूँकि संख्या 2/7 p/q रूप में है, 2√7/7√7 परिमेय है।
(iv) 1/√2
समाधान:
अंश और हर को √2 से गुणा और भाग करने पर हमें प्राप्त होता है,
(1/√2) ×(√2/√2)= √2/2 ( 2×√2 = 2 के बाद से)
हम जानते हैं कि, 2 = 1.4142…
फिर, 2/2 = 1.4142/2 = 0.7071..
चूँकि संख्या 0.7071..अनावश्यक अनावर्ती है, 1/√2 एक अपरिमेय संख्या है।
(वी) 2
समाधान:
हम जानते हैं कि, का मान = 3.1415
अत: 2 = 2×3.1415.. = 6.2830…
चूँकि संख्या, 6.2830…, अनावर्ती अनावर्ती है, 2 एक अपरिमेय संख्या है।
2. निम्नलिखित में से प्रत्येक व्यंजक को सरल कीजिए:
(i) (3+√3)(2+√2)
समाधान:
(3+√3)(2+√2)
कोष्ठकों को खोलने पर, हम पाते हैं, (3×2)+(3×√2)+(√3×2)+(√3×√2)
= 6+3√2+2√3+√6
(ii) (3+√3)(3-√3)
समाधान:
(3+√3)(3-√3) = 32-(√3)2 = 9-3
= 6
(iii) (√5+√2)2
समाधान:
(√5+√2)2 = √52+(2×√5×√2)+ √22
= 5+2×√10+2 = 7+2√10
(iv) (√5-√2)(√5+√2)
समाधान:
(√5-√2)(√5+√2) = (√52-√22) = 5-2 = 3
3. याद कीजिए, को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (जैसे d) के अनुपात के रूप में परिभाषित किया गया है। यानी =c/d. यह इस तथ्य का खंडन करता प्रतीत होता है कि अपरिमेय है। आप इस अंतर्विरोध को कैसे दूर करेंगे?
समाधान:
कोई विरोधाभास नहीं है। जब हम किसी मान को पैमाने से मापते हैं, तो हमें केवल एक अनुमानित मान प्राप्त होता है। हम कभी भी एक सटीक मूल्य प्राप्त नहीं करते हैं। इसलिए, हम यह महसूस नहीं कर सकते हैं कि c या d अपरिमेय है। का मान लगभग 22/7 या 3.142857 के बराबर होता है...
4. संख्या रेखा पर (√9.3) निरूपित करें।
समाधान:
चरण 1: 9.3 इकाई लंबी रेखाखंड, AB खींचिए। AB को C तक इस प्रकार बढ़ाइए कि BC=1 इकाई हो।
चरण 2: अब, AC = 10.3 इकाई। माना AC का केंद्र O है।
चरण 3: त्रिज्या OC का एक अर्धवृत्त बनाएं जिसका केंद्र O है।
चरण 4: बिंदु B पर AC पर एक BD लंबवत खींचिए जो अर्धवृत्त को D पर काटता है। OD को मिलाएँ।
चरण 5: प्राप्त OBD एक समकोण त्रिभुज है।
यहाँ, OD 10.3/2 (अर्धवृत्त की त्रिज्या), OC = 10.3/2, BC = 1
ओबी = ओसी - बीसी
(10.3/2)-1 = 8.3/2
पाइथागोरस प्रमेय का उपयोग करना,
हम पाते हैं,
OD2=BD2+OB2
(10.3/2)2 = BD2+(8.3/2)2
BD2 = (10.3/2)2-(8.3/2)2
(BD)2 = (10.3/2)-(8.3/2)(10.3/2)+(8.3/2)
BD2 = 9.3
बीडी = √9.3
अत: BD की लंबाई √9.3 है।
चरण 6: BD को त्रिज्या और B को केंद्र मानकर एक चाप खींचिए जो रेखाखंड को स्पर्श करता है। जिस बिंदु पर यह रेखा खंड को छूता है वह O से 9.3 की दूरी पर है जैसा कि चित्र में दिखाया गया है।
 |
| ncert solutions for class 9 maths chapter 1 exercise 1.5 |
5. निम्नलिखित के हरों को युक्तिसंगत बनाएं:
(i) 1/√7
समाधान:
1/√7 को √7 . से गुणा और भाग दें
(1×√7)/(√7×√7) = √7/7
(ii) 1/(√7-√6)
समाधान:
1/(√7-√6) को (√7+√6) से गुणा और भाग दें
[1/(√7-√6)]×(√7+√6)/(√7+√6) = (√7+√6)/(√7-√6)(√7+√6)
= (√7+√6)/√72-√62 [हर संपत्ति द्वारा प्राप्त किया जाता है, (a+b)(a-b) = a2-b2]
= (√7+√6)/(7-6)
= (√7+√6)/1
= √7+√6
(iii) 1/(√5+√2)
समाधान:
1/(√5+√2) को (√5-√2) से गुणा और भाग करें
[1/(√5+√2)]×(√5-√2)/(√5-√2) = (√5-√2)/(√5+√2)(√5-√2)
= (√5-√2)/(√52-√22) [हर संपत्ति द्वारा प्राप्त किया जाता है, (a+b)(a-b) = a2-b2]
= (√5-√2)/(5-2)
= (√5-√2)/3
(iv) 1/(√7-2)
समाधान:
1/(√7-2) को (√7+2) से गुणा और भाग दें
1/(√7-2)×(√7+2)/(√7+2) = (√7+2)/(√7-2)(√7+2)
= (√7+2)/(√72-22) [हर गुण से प्राप्त होता है, (a+b)(a-b) = a2-b2]
= (√7+2)/(7-4)
= (√7+2)/3
ncert solutions for class 9 maths chapter 1 exercise 1.6
1. खोजें:
(i)641/2
समाधान:
641/2 = (8×8)1/2
= (82)½
= 81 [⸪2×1/2 = 2/2 =1]
= 8
(ii)321/5
समाधान:
321/5 = (25)1/5
= (25)⅕
= 21 [⸪5×1/5 = 1]
= 2
(iii)1251/3
समाधान:
(125)1/3 = (5×5×5)1/3
= (53)⅓
= 51 (3×1/3 = 3/3 = 1)
= 5
2. खोजें:
(i) 93/2
समाधान:
93/2 = (3×3)3/2
= (32)3/2
= 33 [⸪2×3/2 = 3]
=27
(ii) 322/5
समाधान:
322/5 = (2×2×2×2×2)2/5
= (25)2⁄5
= 22 [⸪5×2/5= 2]
= 4
(iii)163/4
समाधान:
163/4 = (2×2×2×2)3/4
= (24)3⁄4
= 23 [⸪4×3/4 = 3]
= 8
(iv) 125-1/3
(iv) 125-1/3
125-1/3 = (5×5×5)-1/3
= (53)-1⁄3
= 5-1 [⸪3×-1/3 = -1]
= 1/5
3. सरल करें:
(i) 2^2/3×2^1/5
समाधान:
2^2/3×2^1/5 = 2(2/3)+(1/5)[⸪चूंकि, am×an=am+n____ घातांक के नियम]
= 2^13/15 [⸪2/3 + 1/5 = (2×5+3×1)/(3×5) = 13/15]
(ii) (1/3^3)^7
समाधान:
(1/3^3)^7 = (3-3)7 [⸪चूंकि,(am)n = am x n____ घातांक के नियम]
= 3-21
(iii) 111/2/111/4
समाधान:
(11)^1/2/(11)^1/4 = (11)^(1/2)-(1/4)
= 11^1/4 [⸪(1/2) - (1/4) = (1×4-2×1)/(2×4) = 4-2)/8 = 2/8 = ¼ ]
(iv)71/2×81/2
समाधान:
71/2×81/2= (7×8)^1/2 [⸪चूंकि, (am×bm = (a×b)m ____ घातांक के नियम]
= (56)^1/2






.png)
.png)




No comments:
Post a Comment