Download PDF For exponents and powers class 8 in Hindi - Math Notes

Exponents and Powers Class 8 Notes: Chapter 12

घातांक और शक्तियाँ कक्षा 8 अध्याय 12 के लिए यहाँ दिए गए नोट्स उत्पादकता को बढ़ावा देने और विषयों के बारे में समग्र ज्ञान में सुधार करने के लिए एक महान अध्ययन उपकरण हैं। 8वीं कक्षा में, प्रतिपादकों की अवधारणा, शक्तियों और वास्तविक दुनिया में उनके अनुप्रयोगों को स्पष्ट रूप से समझाया गया है। यह अध्याय छात्रों को प्रतिपादकों और शक्तियों की अवधारणा पर एक मजबूत आधार बनाने में मदद करता है। बेहतर समझ के लिए हल और उदाहरण की समस्याएं यहां दी गई हैं। छात्र इन नोट्स का उपयोग पूरे अध्याय का गहन पुनरीक्षण करने के लिए कर सकते हैं और साथ ही परीक्षा लिखने के लिए अच्छी तरह से सुसज्जित हो सकते हैं।

exponents and powers class 8 pdf : Powers and Exponents

किसी संख्या की घात यह दर्शाती है कि उसे कितनी बार गुणा करना है। यह एबी के रूप में लिखा गया है। जहां 'बी' इंगित करता है कि हमारे परिणाम प्राप्त करने के लिए 'ए' को कितनी बार गुणा करने की आवश्यकता है। यहाँ 'a' को आधार और 'b' को घातांक कहते हैं।

उदाहरण के लिए: 9³ पर विचार करें। यहां घातांक '3' इंगित करता है कि आधार '9' को हमारे समकक्ष उत्तर प्राप्त करने के लिए तीन बार गुणा करने की आवश्यकता है जो कि 27 है।

Powers with Negative Exponents

किसी भी गैर-पूर्णांक के लिए सत्ता में एक नकारात्मक घातांक मूल रूप से शक्ति का पारस्परिक है।

सरल शब्दों में, एक घातांक -b के साथ एक शून्येतर पूर्णांक a के लिए,
-b, a^-b = 1^ab

exponents and powers class 8 pdf : Visualising Powers and Exponents

संख्याओं की शक्तियों को आकृतियों और आकृतियों के रूप में आसानी से देखा जा सकता है। निम्नलिखित विज़ुअलाइज़ेशन पर विचार करें।

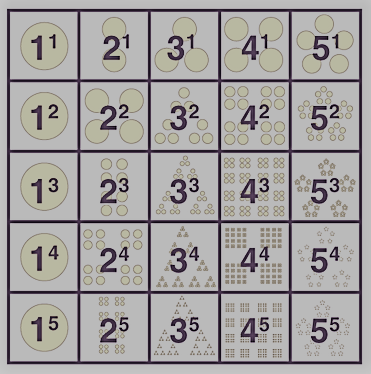exponents and powers class 8 pdf

exponents and powers class 8 : Expanding a Rational Number Using Powers

दी गई परिमेय संख्या को घातांकों की सहायता से विस्तारित रूप में व्यक्त किया जा सकता है। एक संख्या 1204.65 पर विचार करें। विस्तारित होने पर संख्या को इस प्रकार लिखा जा सकता है:
1204.65=1000+200+4+0.6+0.05=(1×10³)+(2×10²)+(0×10¹)+(4×10-¹)+(5×10-²)

 

exponents and powers class 8 : Laws of Exponents

Exponents with like Bases

एक गैर-शून्य पूर्णांक दिया गया है, a^m×aⁿ=a^m+n जहां m और n पूर्णांक हैं।

और a^m÷aⁿ=a^m−n जहां m और n पूर्णांक हैं।

उदाहरण के लिए: 2³×2⁷ = 2^{7 + 3} = 2¹⁰
और 2⁷2³ = 2⁷⁻³ 

Power of a Power

एक शून्येतर पूर्णांक a, (a^m)ⁿ = a^mn दिया गया है, जहाँ m और n पूर्णांक हैं।

उदाहरण के लिए: (2⁴)³ = 2^4×3 = 2¹² एक गैर-शून्य पूर्णांक दिया गया है,

(a)0 = 1 घात 0 के लिए कोई भी संख्या हमेशा 1 होती है।

exponents and powers class 8  :  Exponents with Unlike Bases and Same Exponent

दो शून्येतर पूर्णांक a और b दिए हुए हैं,

a^m×b^m = (a×b)^m, जहाँ m एक पूर्णांक है।

उदाहरण के लिए: 2³×5³ = (2×5)³ = 10³ = 1000

exponents and powers class 8 : Uses of Exponents

Inter Conversion between Standard and Normal Forms

exponents and powers class 8

बहुत बड़ी या बहुत छोटी संख्याओं को घातांकों की सहायता से मानक रूप में निरूपित किया जा सकता है।

यदि यह 150,000,000,000 जैसी बहुत बड़ी संख्या है, तो हमें दशमलव स्थान को बाईं ओर ले जाने की आवश्यकता है। और जब हम ऐसा करेंगे तो घातांक धनात्मक होगा।

                                                                          

चूँकि दशमलव को 1 और 5 के बीच रखने तक 11 स्थान ले जाया जाता है, बड़ी संख्या का हमारा मानक रूप प्रतिनिधित्व 1.5×1011 होगा

यदि यह 0.000007 जैसी बहुत छोटी संख्या है, तो हमें दशमलव स्थानों को उसके मानक रूप में दर्शाने के क्रम में दाईं ओर ले जाने की आवश्यकता है। दाईं ओर स्थानांतरित होने पर, घातांक ऋणात्मक होगा।

exponents and powers class 8

इस स्थिति में, दशमलव स्थान को 6 स्थान ऊपर ले जाया जाता है जब तक कि इसे अंक 7 के बाद नहीं रखा जाता है। इसलिए हमारा मानक रूप प्रतिनिधित्व होगा

7×10⁻⁶
संख्या को उसके मानक रूप से उसके प्राकृतिक रूप में परिवर्तित करते समय घातांक भी उपयोगी होते हैं।

Comparison of Quantities Using Exponents

दो बड़ी या छोटी मात्राओं की तुलना करने के लिए, हम उन्हें उनके मानक घातांक रूप में परिवर्तित करते हैं और उन्हें विभाजित करते हैं।

उदाहरण के लिए: पृथ्वी के व्यास और सूर्य के व्यास की तुलना करना।

पृथ्वी का व्यास = 1.2756 × 10⁶m
सूर्य का व्यास =1.4×10⁹m
पृथ्वी का व्यास = 1.4×10⁹m
1.2756 × 10⁷m=109

तो सूर्य का व्यास पृथ्वी के व्यास का 109 गुना है! कुल या दो राशियों के बीच के अंतर की गणना करते समय, हमें पहले यह सुनिश्चित करना चाहिए कि दोनों मात्राओं के घातांक समान हों।