Download PDF For class 11 Chapter 10 Notes in Hindi - Physics Notes in Hindi

 

mechanical properties of fluids class 11 notes

• तरल पदार्थ वे पदार्थ हैं जो प्रवाहित हो सकते हैं जैसे, तरल पदार्थ और गैसें। इसका कोई निश्चित आकार नहीं होता है।

• जब कोई वस्तु आराम से द्रव में डूबी होती है, तो द्रव सामान्य रूप से अपनी सतह पर एक बल लगाता है। इसे द्रव का प्रणोद कहते हैं।

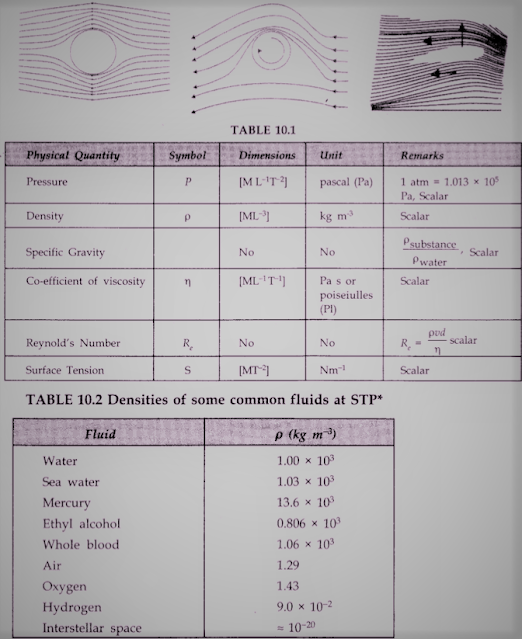
Pressure

 विरामावस्था में द्रव की सतह के प्रति इकाई क्षेत्रफल पर लगने वाले बल को दाब कहते हैं।

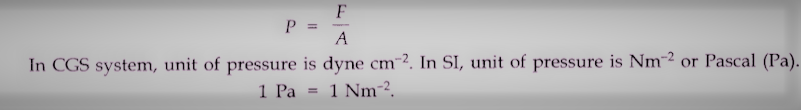mechanical properties of fluids class 11 notes

• जब कोई द्रव साम्यावस्था में होता है, तो उसकी सतह पर कार्य करने वाला बल हर जगह लंबवत होता है। दबाव समान क्षैतिज स्तर पर समान होता है।

• द्रव में किसी भी बिंदु पर दबाव सतह के नीचे की गहराई (एच), तरल के घनत्व और गुरुत्वाकर्षण के कारण त्वरण पर निर्भर करता है।

physics notes for class 11 pdf : Pascal’s Law

 पास्कल के नियम के अनुसार, एक बंद तरल पर लगाया जाने वाला दबाव तरल के हर हिस्से और युक्त बर्तन की दीवारों पर कम से कम प्रसारित होता है।

• हाइड्रोलिक सिस्टम पास्कल के नियम पर काम करता है। क्षेत्रफल पर लगाया गया बल, सभी अनुप्रस्थ काटों पर अनुपात समान होगा।

physics notes for class 11 pdf

नोट: बड़े क्रॉस-सेक्शन में एक बड़े बल का अनुभव होता है, एक छोटा बल 4क्रॉस को रिलेशन सेक्शन द्वारा छोटे में लगाया जाता है।
• घनत्व p के तरल की ऊंचाई h का एक स्तंभ एक दबाव P देता है जो दिया गया है

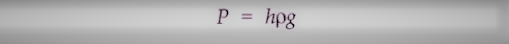class 11 physics notes pdf

• यदि Pa वायुमंडलीय दबाव हो तो किसी द्रव में उसकी मुक्त सतह से h गहराई पर दबाव P = Pa+ hρg द्वारा दिया जाता है। संबंध केवल असंपीड्य द्रवों के लिए सत्य है।

• गेज दबाव (पीजी), निरपेक्ष दबाव (पी) और वायुमंडलीय दबाव (पीए) का अंतर है।

निरपेक्ष दबाव (P) = गेज दबाव (Pg) + वायुमंडलीय दबाव (Pa)

P_g=P-P_a

mechanical properties of solids ncert solutions Archimedes Principle

 जब कोई पिंड आंशिक रूप से या पूरी तरह से तरल में डूबा होता है, तो उसका कुछ वजन कम हो जाता है। हानि
तरल में शरीर के वजन में डूबे हुए द्वारा विस्थापित तरल के वजन के बराबर है शरीर का अंग।

• जब कोई पिंड डुबोया जाता है तो तरल द्वारा विस्थापित ऊपर की ओर बल उत्प्लावन कहलाता है। इसके कारण, शरीर द्वारा अनुभव किए गए वजन में स्पष्ट कमी होती है।

 
• Law of Floatation- एक पिंड एक तरल में तैरता है यदि शरीर के डूबे हुए हिस्से द्वारा विस्थापित तरल का वजन शरीर के वजन के बराबर हो।"

. जब कोई पिंड किसी द्रव में आंशिक या पूर्ण रूप से डुबाया जाता है, तो शरीर पर कार्य करने वाले विभिन्न बल होते हैं
(i) उर्ध्व प्रणोद (T) उत्प्लावकता के केंद्र पर कार्य कर रहा है और जिसका परिमाण के बराबर है विस्थापित तरल का वजन और

 (ii) पिंड का भार (W) जो अपने गुरुत्वाकर्षण केंद्र के माध्यम से लंबवत नीचे की ओर कार्य करता है।
(a) जब डब्ल्यू> टी, शरीर तरल में डूब जाएगा;
(b) जब डब्ल्यू = टी, तो शरीर तरल के अंदर संतुलन में रहेगा;
(c) जब डब्ल्यू <टी, तो शरीर तरल की सतह तक आ जाएगा इस तरह से डूबे हुए हिस्से के कारण विस्थापित तरल का वजन शरीर के वजन के बराबर होता है। इस प्रकार शरीर तैरता रहेगा और इसका केवल एक हिस्सा तरल के अंदर डूबा रहेगा।

• द्रव के प्रवाह को स्थिर या धारा रेखा प्रवाह कहा जाता है यदि द्रव का ऐसा कण गुजर रहा हो किसी दिए गए बिंदु के माध्यम से उसी पथ के साथ और उसी गति के साथ यात्रा करता है जैसे पिछले कण उसी बिंदु से गुजरते हैं।

• यदि तरल विभिन्न वेगों की परतों के रूप में एक क्षैतिज सतह पर बहता है, तो तरल के प्रवाह को लामिना का प्रवाह कहा जाता है।

• द्रव का वह प्रवाह जिसमें किसी दिए गए बिंदु को पार करने वाले सभी कणों का वेग समान नहीं होता और द्रव की गति अनियमित या अव्यवस्थित हो जाती है, अशांत प्रवाह कहलाता है।

mechanical properties of fluids class 11 notes Equation of Continuity

 निरंतरता के समीकरण के अनुसार, यदि पाइप की लंबाई के साथ कोई तरल स्रोत या सिंक नहीं है, तो प्रति यूनिट समय में पाइप के किसी भी हिस्से को पार करने वाले द्रव का द्रव्यमान स्थिर रहता है। यानी„ a1 v1ρ1 = a2v2 ρ2
असंपीड्य द्रवों (अर्थात द्रवों) के लिए ρ1 = 2 और इसलिए समीकरण इस प्रकार दिया गया है
a1v1=a2v2
- इसका मतलब है कि जहां पाइप संकरा होता है और प्रवाह की गति कम होती है वहां तरल के प्रवाह की गति अधिक होती है
जहां पाइप का क्रॉस-सेक्शन अधिक है।

chapter 10 physics class 11 notes Energy of a liquid

 एक तरल में तीन प्रकार की ऊर्जा हो सकती है: 

(i) गतिज ऊर्जा, (ii) स्थितिज ऊर्जा और (iii) दबाव ऊर्जा
किसी द्रव में उसकी गति के कारण जो ऊर्जा होती है, उसे गतिज ऊर्जा कहते हैं, अर्थात् 

                   1/2mv2
ऊँचाई h पर m द्रव्यमान वाले किसी द्रव की स्थितिज ऊर्जा P.E द्वारा दी जाती है। = mgh
किसी द्रव में उसके दाब के कारण जो ऊर्जा होती है उसे दाब ऊर्जा कहते हैं। मात्रा dV = PdV . में तरल की दबाव ऊर्जा
तरल के प्रति इकाई द्रव्यमान में दबाव ऊर्जा

chapter 10 physics class 11 notes

• Bernoulli’s Theorem

 एक असंपीड्य, गैर-चिपचिपा, इरोटेशनल तरल जिसमें सुव्यवस्थित प्रवाह होता है, दबाव ऊर्जा, गतिज ऊर्जा और प्रति इकाई द्रव्यमान की स्थितिज ऊर्जा का योग एक स्थिरांक होता है, अर्थात,

Bernoulli’s Theorem

mechanical properties of solids NCERT solutions :- Viscosity

 श्यानता द्रव (तरल या गैस) का वह गुण है जिसके कारण द्रव सापेक्ष गति वाली परतों के रूप में गति में होने पर एक आंतरिक घर्षण बल काम में आता है। यह विभिन्न परतों की सापेक्ष गति का विरोध करता है। श्यानता को द्रव घर्षण भी कहते हैं।

Viscosity

• श्यान बल सीधे परत के क्षेत्र और वेग प्रवणता पर निर्भर करता है।

• Coefficient of Viscosity

Coefficient of Viscosity

 किसी द्रव का श्यानता गुणांक उस स्पर्शरेखा बल के बराबर होता है जो प्रत्येक क्षेत्र एकता वाले द्रव की दो समानांतर परतों के बीच एकांक वेग प्रवणता बनाए रखने के लिए आवश्यक होता है।

श्यानता गुणांक का SI मात्रक poiseuille (Pl) या Pa - s या Nm-2 s या kg m-1 s-1 है। q का विमीय सूत्र [ML-1T-1] है।

chapter 10 physics class 11 notes : Stoke’s Law

 स्टोक्स के नियम के अनुसार r त्रिज्या के एक छोटे गोलाकार पिंड पर कार्य करने वाला पिछड़ा खींचने वाला बल v वेग के साथ चिपचिपापन के गुणांक के एक चिपचिपा माध्यम के माध्यम से चलता है द्वारा दिया गया है
                                               F = 6πήr

• Terminal Velocity

 यह एक श्यान माध्यम में स्वतंत्र रूप से गिरते समय शरीर द्वारा प्राप्त अधिकतम स्थिर वेग है। यह तब प्राप्त होता है जब चिपचिपा बल द्वारा स्पष्ट वजन की भरपाई की जाती है।
यह द्वारा दिया गया है

• Terminal Velocity

जहाँ p त्रिज्या r के पिंड की सामग्री का घनत्व हो और o माध्यम का घनत्व हो।

mechanical properties of fluids class 11 notes :- Poiseuille’s Equation

 पॉईसुइल के अनुसार, यदि लंबाई 'l' और त्रिज्या 'r' की केशिका ट्यूब के दोनों सिरों पर दबाव अंतर (P) बनाए रखा जाता है, तो प्रति सेकंड ट्यूब से निकलने वाले तरल का आयतन दबाव के सीधे आनुपातिक होता है अंतर (P)।
(ii) केशिका नली की त्रिज्या (r) की चौथी शक्ति के सीधे आनुपातिक।
(iii) द्रव के श्यानता गुणांक (ή) के व्युत्क्रमानुपाती होता है।
(iv) केशिका नली की लंबाई (i) के व्युत्क्रमानुपाती।
यह के रूप में दिया जाता है

mechanical properties of fluids class 11 notes :- Poiseuille’s Equation

• Reynold’s Number

 रेनॉल्ड नंबर रे एक आयामहीन संख्या है जिसका मान एक अनुमानित विचार देता है कि क्या द्रव का प्रवाह सुव्यवस्थित या अशांत होगा। यह द्वारा दिया गया है

• Reynold’s Number

जहाँ p = गति u के साथ बहने वाले द्रव का घनत्व, d पाइप के व्यास के लिए है और q द्रव की चिपचिपाहट है। किसी भी इकाई निकाय में Re का मान समान रहता है।

• यह देखा गया है कि प्रवाह रे <= 1000 के लिए स्ट्रीमलाइन या लैमिनार है और प्रवाह रे> = 2000 के लिए अशांत है। प्रवाह 1000 और 2000 के बीच रे के लिए अस्थिर हो जाता है। रे का महत्वपूर्ण मूल्य, जिस पर अशांति सेट होती है, वही है ज्यामितीय रूप से समान प्रवाह के लिए।

• पुनः को जड़त्वीय बल (जड़ता के कारण बल अर्थात गतिमान द्रव का द्रव्यमान या उसके मार्ग में बाधा की जड़ता के कारण) के अनुपात के रूप में भी व्यक्त किया जा सकता है, अर्थात,

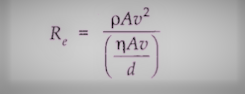class 11 physics notes in hindi

 class 11 physics notes in hindi :- Critical Velocity

 क्रांतिक वेग द्रव प्रवाह का वह वेग है, जिस तक उसका प्रवाह सुव्यवस्थित होता है और जिसके ऊपर उसका प्रवाह अशांत हो जाता है।
यह द्वारा दिया गया है

 class 11 physics notes in hindi :- Critical Velocity

जहाँ K एक विमाहीन स्थिरांक है, q द्रव की श्यानता का गुणांक है, p द्रव का घनत्व है और r नली की त्रिज्या है।

mechanical properties of fluids class 11 notes PDF :- Surface Tension 

यह द्रव का वह गुण है जिसके कारण विरामावस्था में द्रव की मुक्त सतह का क्षेत्रफल न्यूनतम होता है और इस प्रकार यह एक तनी हुई लोचदार झिल्ली के रूप में व्यवहार करता है।

• तरल सतह पर खींची गई रेखा की प्रति इकाई लंबाई और सतह के समानांतर उसके समानांतर कार्य करने वाले बल को सतह तनाव का बल कहा जाता है।

पृष्ठ तनाव का SI मात्रक Nm-1 है और इसका विमीय सूत्र [MT-2] है,

class 11 physics notes in Hindi :- Surface Energy

 द्रव के पृष्ठ में निहित ऊर्जा को पृष्ठीय ऊर्जा कहते हैं। सतही ऊर्जा में परिवर्तन सतही तनाव और निरंतर तापमान के तहत सतह क्षेत्र में परिवर्तन का उत्पाद है।

• त्रिज्या r की एक केशिका नली में पानी जिस ऊँचाई तक ऊपर उठता है, वह किसके द्वारा दिया जाता है?

class 11 physics notes in Hindi :- Surface Energy

जहाँ T द्रव का पृष्ठ तनाव है और 0 संपर्क कोण है।
सतही तनाव के कारण एक तरल ओवर की सतह फिल्म के अवतल पक्ष पर अतिरिक्त दबाव होता है

उत्तल पक्ष और 2T/r के बराबर है। साबुन के बुलबुले के लिए अतिरिक्त दबाव 4T/r है, जहां r सतह की त्रिज्या को दर्शाता है।

• Angle of Contact

 संपर्क के बिंदु पर तरल सतह के लिए स्पर्शरेखा जो कोण तरल के अंदर ठोस सतह के साथ बनाता है उसे संपर्क कोण कहा जाता है।

एक ही पदार्थ के अणुओं के बीच लगने वाले अंतराआण्विक बल को संसजन बल कहते हैं। हालाँकि, विभिन्न पदार्थों के अणुओं के बीच लगने वाले बल को आसंजन बल कहा जाता है।

• Torricelli’s Theorem

 इस प्रमेय के अनुसार, बहिर्वाह का वेग अर्थात जिस वेग से द्रव छिद्र से बाहर निकलता है {अर्थात, एक संकीर्ण छिद्र) उस वेग के बराबर होता है जो एक स्वतंत्र रूप से गिरने वाला पिंड ________ की गहराई के बराबर एक ऊर्ध्वाधर दूरी से गिरने में प्राप्त करता है। तरल की मुक्त सतह के नीचे छिद्र।
वेग द्वारा दिया गया है
V = √2gh

mechanical properties of fluids class 11 notes : Magnus Effect

 जब एक गेंद को हवा के अणुओं की धारा में होने पर स्पिन दिया जाता है, तो यह एक घुमावदार पथ का अनुसरण करेगी जो अधिक दबाव वाले पक्ष की ओर उत्तल है। यह विचार स्पिन गेंदबाजों से गेंद को लिफ्ट और वायुगतिकी प्राप्त करने का आधार है। 

mechanical properties of fluids class 11 notes : Magnus Effect

mechanical properties of fluids class 11 notes