NCERT Solutions for Class 9 Math Chapter 9 in Hindi

ncert solutions for class 9 maths chapter 9 exercise 9.1

Ex 9.1 कक्षा 9 गणित प्रश्न 1

निम्नलिखित में से कौन सी आकृति एक ही आधार पर और समान समांतर रेखाओं के बीच स्थित है। ऐसी स्थिति में उभयनिष्ठ आधार और दो समांतर लिखिए।

ncert solutions for class 9 maths chapter 9

समाधान:

आकृतियाँ (i), (iii) और (v) एक ही आधार पर और एक ही समान्तर रेखाओं के बीच स्थित हैं।

ncert solutions for class 9 maths chapte

NCERT Solutions for Class 9 Maths Chapter 9  Ex 9.2

Ex 9.2 कक्षा 9 गणित प्रश्न 1.

आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC  और CF ⊥ AD.। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।

ncert solutions for class 9 maths chapter 9

समाधान:

BSOहमारे पास है, AE ⊥ DC  और AB = 16 सेमी

AB = CD [समानांतर चतुर्भुज की विपरीत भुजाएँ]

∴ सीडी = 16 सेमी

अब, समांतर चतुर्भुज ABCD का क्षेत्रफल = CD x AE

= (16 x 8) सेमी2 = 128 सेमी2 [∵ एई = 8 सेमी]

चूँकि, CF ⊥ AD

समांतर चतुर्भुज ABCD का क्षेत्रफल = AD x CF

AD x CF = 128 सेमी

AD x 10 सेमी = 128 सेमी2 [∵ CF= 10 सेमी]

AD = 128/10 सेमी = 12.8 सेमी 10

अत: AD की अभीष्ट लंबाई 12.8 cm . है

Ex 9.2 कक्षा 9 गणित प्रश्न 2.

यदि E, F, G और H क्रमशः समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = 12 ar (ABCD) है।

समाधान:

GE और HE को मिलाइए, जहां GE || BC || DAऔर  HF || AB || DC

(∵ E, F, G और H एक ||gm ABCD की भुजाओं के मध्य बिन्दु हैं)।

यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समान्तर रेखाओं के बीच में हों, तो A E U त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल के आधे के बराबर होता है।

ncert solutions for class 9 maths chapter 9 q.2

अब, EFG और समांतर चतुर्भुज EBCG एक ही आधार EG और एक ही समान्तर रेखाओं EG और BC के बीच स्थित हैं।

ar(∆EFG) = 12ar(∥gmEBCG) … (1)

इसी तरह, (∆EHG) = 

12ar(∥gmAEGD) …(2)

(1) और (2) को जोड़ने पर, हमें प्राप्त होता है

ar(∆EFG) + ar(∆EHG) = 12ar(∥gmEBCG)+12ar(∥gmAEGD)
= 12ar(∥gmABCD)

अत: ar(EFGH) = 

12ar(ABCD)

Ex 9.2 कक्षा 9 गणित प्रश्न 3.

P और Q एक समांतर चतुर्भुज ABCD के क्रमशः DC और AD भुजाओं पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।

समाधान:

ABCD एक समांतर चतुर्भुज है।

∴ AB || CD और BC || AD.

अब, APB और समांतर चतुर्भुज ABCD एक ही आधार AB पर और एक ही समान्तर रेखाओं AB और CD के बीच स्थित हैं।

ar(∆APB) =  12ar(∥gmABCD) …….(1) 

ncert solutions for class 9 maths chapter 9 

साथ ही, BQC और समांतर चतुर्भुज ABCD एक ही आधार BC पर और एक ही समांतर रेखाओं BG और AD के बीच स्थित हैं।

ar(∆BQC) =12ar(∥gmABCD)…(2)

(1) और (2) से, हमारे पास ar(∆APB) = ar(∆BQC) है।

Ex 9.2 कक्षा 9 गणित प्रश्न 4.

आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में एक बिंदु है। वो दिखाओ

ncert solutions for class 9 maths chapter 9 in Hindi

(i) ar (APB) + ar (PCD) = 1/2ar (ABCD)

(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)

समाधान:

हमारे पास एक समांतर चतुर्भुज ABCD है, अर्थात् AB || सीडी और  BC || AD आइए हम EF ड्रा करें  EF || AB  और एचजी || एडी के माध्यम से पी.

ncert solutions for class 9 maths in hindi medium pdf

(i) APB और ||gm AEFB एक ही आधार AB पर और एक ही समांतर रेखाओं AB और EF के बीच स्थित हैं।

ar(∆APB) = 

12ar(∥gmAEFB) …(1)

साथ ही, PCD और समांतर चतुर्भुज CDEF एक ही आधार CD पर और एक ही समांतर CD और EF के बीच स्थित हैं।

ar(APCD) = 12ar(∥gmCDEF) …(2)

(1) और (2) को जोड़ने पर, हमारे पास है

ar(∆APB) + ar(∆PCD) = 12ar(∥gmAEFB)+12ar(∥gmCDEF)
⇒ ar(∆APB) + ar(∆PCD) = 12ar(∥gmABCD) …(3)

(ii) ∆APD और ||gm DGH एक ही आधार AD पर और एक ही समान्तर रेखाओं AD और GH के बीच स्थित हैं।

∴ ar(∆APD) = 12ar(∥gmADGH) …(4)

इसी तरह,

ar(∆PBC) = 12ar(∥gmBCGH) …(5)

(4) और (5) को जोड़ने पर, हमारे पास है

ar(∆APD) + ar(∆PBC) = = 12ar(∥gmADGH)+12ar(∥gmBCGH)
⇒ ar(∆APD) + ar(∆PBC) =12ar(∥gmABCD) …….(6)

(3) और (6) से, हमारे पास है

ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

Ex 9.2 कक्षा 9 गणित प्रश्न 5.

आकृति में, PQRS और ABRS समांतर चतुर्भुज हैं और X भुजा BR पर स्थित कोई बिंदु है। वो दिखाओ

(i) ar (PQRS) = ar (ABRS)

(ii) ar (AXS) = 1/2ar(PQRS)

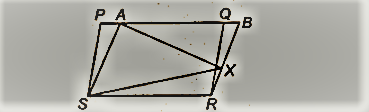cbse class 9 maths chapter 9 exercise 9.2 solution

समाधान:

(i) समांतर चतुर्भुज PQRS और समांतर चतुर्भुज ABRS एक ही आधार RS पर और समान समांतर रेखाओं RS और PB के बीच स्थित हैं।

ar(PQRS) = ar(ABRS)

(ii) AAXS और ||gm ABRS एक ही आधार AS पर और एक ही समान्तर रेखाओं AS और BR के बीच स्थित हैं। *

ar(AXS) = 1/2ar(ABRS) …(1)

परंतु ar(PQRS) = ar(ABRS) …(2) [(i) भाग में सिद्ध]

(1) और (2) से, हमारे पास है

ar(AXS) = 1/2ar(PQRS)

Ex 9.2 कक्षा 9 गणित प्रश्न 6.

एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। खेतों को कितने भागों में बांटा गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए।

समाधान:

किसान के पास खेत समानांतर चतुर्भुज PQRS के रूप में है और एक बिंदु A RS पर स्थित है। AP और AQ को मिलाइए।

स्पष्ट रूप से, क्षेत्र को तीन भागों में विभाजित किया गया है, अर्थात ∆APS, PAQ और QAR में।

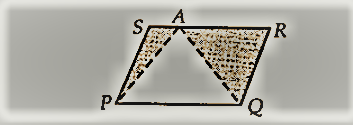cbse class 9 maths chapter 9 exercise 9.2 solution in hindi

चूँकि, PAQ और pt.

समांतर चतुर्भुज PQRS एक ही आधार PQ पर और समान समानांतर PQ और RS के बीच स्थित हैं।

ar(∆PAQ) = 12ar(∥gmPQRS) …(1)
⇒ ar(||gm PQRS) – ar(∆PAQ) = ar(||gm PQRS) – 12ar(∥gmPQRS)
⇒ [ar(∆APS) + ar(∆QAR)] = 12ar(∥gmPQRS) …(2)

(1) और (2) से, हमारे पास है

ar(∆PAQ) = ar[(∆APS) + (∆QAR)]

इस प्रकार, किसान (∆PAQ) में गेहूं और [(∆APS) + (∆QAR)] में गेहूं या [(∆APS) + (∆QAR)] में गेहूं और (∆PAQ) में दालें बो सकता है।

cbse class 9 maths chapter 9 exercise 9.3 solution

Ex 9.3 कक्षा 9 गणित प्रश्न 1.

आकृति में, E एक ABC की माध्यिका AD पर स्थित कोई बिंदु है। दर्शाइए कि ar (ABE) = ar (ACE) है।

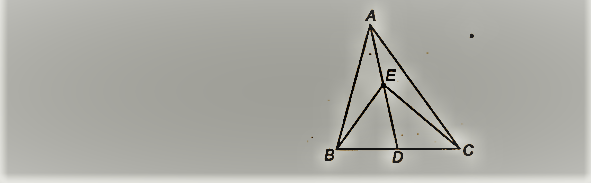cbse class 9 maths chapter 9 exercise 9.2 solution

समाधान:

हमारे पास एक ABC इस प्रकार है कि AD एक माध्यिका है।

ar(∆ABD) = ar(∆ACD) …(1)

[∵ एक माध्यिका त्रिभुज को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है]

इसी तरह, BEC में, हमारे पास है

ar(∆BED) = ar(∆DEC) …(2)

(2) को (1) से घटाने पर हमें प्राप्त होता है

ar(∆ABD) - ar(∆BED) = ar(∆ACD) - ar(∆DEC)

ar(∆ABE) = ar(∆ACE)।

Ex 9.3 कक्षा 9 गणित प्रश्न 2.

एक त्रिभुज ABC में, E माध्यिका AD का मध्य-बिंदु है। दिखाएँ कि  ax (BED) =  12ar(ABC)

समाधान:

हमारे पास एक ∆ABC और उसकी माध्यिका AD है।

आइए हम B और E को मिलाएँ।

NCERT Solutions for Class 9 Maths Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.3 Q2

चूँकि एक माध्यिका त्रिभुज को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।

ar (∆ABD) = 1/2ar(ΔABC) …….(1)

अब, ABD में, BE एक माध्यिका है।

[ E, AD का मध्य-बिंदु है]

ar(∆BED) = 1/2ar(ΔABC) …(2)

(1) और (2) से, हमारे पास है

ar(∆BED) = 1/2 [12ar(ΔABC)]

ar(∆BED) = 1/4ar(ΔABC)

Ex 9.3 कक्षा 9 गणित प्रश्न 3.

दिखाएँ कि एक समांतर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं।

समाधान:

हमारे पास एक समांतर चतुर्भुज ABCD है (मान लीजिए)

इस प्रकार कि इसके विकर्ण O पर प्रतिच्छेद करते हैं।

समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।

AO = OC और BO = OD

आइए हम CE BD खींचते हैं।

अब, ar(∆BOC) = 1/2BO x CE और

एआर(∆DOC) = 1/2OD x CE

cbse class 9 maths chapter 9 exercise 9.2 solution q.3

चूँकि, BO = OD

ar(∆BOC) = ar(∆DOC) …(1)

इसी तरह, ar(∆AOD) = ar(∆DOC) …(2)

और ar(∆AOB) = ar(∆BOC) …(3)

(1), (2) और (3) से, हमारे पास है

ar(∆AOB) = ar(∆BOC) = ar(∆COD) = ar(∆DOA)

इस प्रकार, एक समांतर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं।

Ex 9.3 कक्षा 9 गणित प्रश्न 4.

आकृति में, ABC और ABD एक ही आधार AB पर स्थित दो त्रिभुज हैं। यदि रेखा खंड CD को AB द्वारा O पर समद्विभाजित किया जाता है, तो दर्शाइए कि ar(ABC) = ar(ABD)

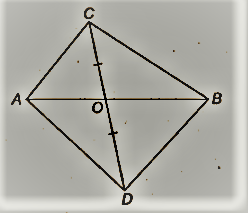cbse class 9 maths chapter 9 exercise 9.2 solution q.4

समाधान:

हमारे पास ABC और ABD एक ही आधार AB पर हैं।

∵ CD, O पर समद्विभाजित है। [दिया है]

सीओ = ओडी

अब, ACD में, AO एक माध्यिका है

ar(∆OAC) = ar(∆OAD) …(1)

पुनः, BCD में, BO एक माध्यिका है

ar(∆OBC) = ar(∆ODB) …(2)

(1) और (2) को जोड़ने पर, हमारे पास है

ar(∆OAQ + ar(∆OBQ) = ar(∆OAD) + ar(∆ODB)

ar(∆ABC) = ar(∆ABD)

Ex 9.3 कक्षा 9 गणित प्रश्न 5.

D,E और F क्रमशः एक ABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। वो दिखाओ

(i) BDEF एक समांतर चतुर्भुज है।

(ii) ar(DEF) = 1/4ar(ABC)

(iii) ar(BDEF) = 1/4ar(ABC)

ncert solutions for class 9 maths chapter 9 ex. 3.3

समाधान:

हमारे पास ∆ABC ऐसा . है

कि D, E और किराया क्रमशः BC, CA और AB के मध्य बिंदु हैं।

ncert solutions for class 9 maths in hindi medium pdf

(i) ABC में, E और F क्रमशः AC और B D C AB के मध्य-बिंदु हैं।

∴ ईएफ || ईसा पूर्व [मध्य-बिंदु प्रमेय]

⇒ ईएफ || बीडी

साथ ही, EF = 1/2(BC)

EF = BD [D, BC का मध्य-बिंदु है]

चूँकि BDEF एक चतुर्भुज है जिसकी सम्मुख भुजाओं का एक युग्म समांतर और समान लंबाई का है।

BDEF एक समांतर चतुर्भुज है।

(ii) हमने सिद्ध किया है कि BDEF एक समांतर चतुर्भुज है।

इसी तरह, DCEF एक समांतर चतुर्भुज है और DEAF भी एक समांतर चतुर्भुज है।

अब, समांतर चतुर्भुज BDEF और समांतर चतुर्भुज DCEF एक ही आधार EF पर और समान समानांतर BC और EF के बीच स्थित हैं।

ar(||gm BDEF) = ar(||gm DCEF)

⇒ 12ar(||gm BDEF) = 12ar(||gm DCEF)

ar(∆BDF) = ar(∆CDE) …(1)

[एक समांतर चतुर्भुज का विकर्ण इसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है]

इसी तरह, ar(∆CDE) = ar(∆DEF) …(2)

और ar(∆AEF) = ar(∆DEF) …(3)

(1), (2) और (3) से, हमारे पास है

ar(∆AEF) = ar(∆FBD) = ar(∆DEF) = ar(∆CDE)

अत: ar(∆ABC) = ar(∆AEF) + ar(∆FBD) + ar(∆DEF) + ar(∆CDE) = 4 ar(∆DEF)

ar(∆DEF) = 1/4ar(∆ABC)

(iii) हमारे पास, ar (||gm BDEF) = ar(∆BDF) + ar(∆DEF) है।

= ar(∆DEF) + ar(∆DEF) [∵ ar(∆DEF) = ar(∆BDF)]

2ar(∆DEF) = 2[1/4ar(∆ABC)]

= 1/2ar(∆ABC)

अत: ar (||gm BDEF) = 

12ar(∆ABC)

Ex 9.3 कक्षा 9 गणित प्रश्न 6.

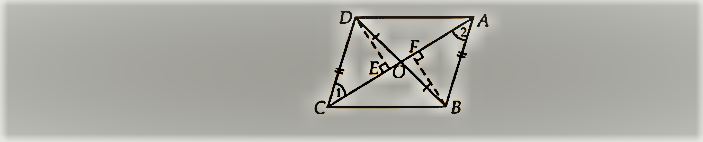
आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD 0 पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि

(i) ar(DOC) = ar(AOB)

(ii) ar (DCB) = ar (ACB)

(iii) डीए || CB या ABCD एक समांतर चतुर्भुज है

cbse class 9 maths chapter 9 exercise 9.2 solution

समाधान:

हमारे पास एक चतुर्भुज ABCD है जिसके विकर्ण AC और BD प्रतिच्छेद करते हैं O पर।

हमारे पास यह भी है कि OB = OD, AB = CD आइए हम DE ⊥ AC और BF AC खींचते हैं।

ncert solutions for class 9 maths chapter 9

(i) DEO और ∆BFO में, हमारे पास है

डीओ = बीओ [दिया गया]

∠DOE = ∠BOF [ऊर्ध्वाधर सम्मुख कोण]

∠DEO = ∠BFO [प्रत्येक 90°]

 ∆DEO ≅ ∆BFO [एक एएस सर्वांगसमता द्वारा]

डीई = बीएफ [सी.पी.सी.टी. द्वारा]

और ar(∆DEO) = ar(∆BFO) …(1)

अब, DEC और BFA में, हमारे पास है

DEC = ∠BFA [प्रत्येक 90°]

डीई = बीएफ [उपरोक्त सिद्ध]

डीसी = बीए [दिया गया]

DEC ∆BFA [RHS सर्वांगसमता द्वारा]

ar(∆DEC) = ar(∆BFA) …(2)

और 1 = ∠2 …(3) [सी.पी.सी.टी. द्वारा]

(1) और (2) को जोड़ने पर, हमारे पास है

ar(∆DEO) + ar(∆DEC) = ar(∆BFO) + ar(∆BFA)

ar(∆DOC) = ar(∆AOB)

(ii) चूँकि, ar(∆DOC) = ar(∆AOB) [उपरोक्त सिद्ध]

दोनों पक्षों में ar(∆BOC) जोड़ने पर, हमें प्राप्त होता है

ar(∆DOC) + ar(∆BOC) = ar(∆AOB) + ar(∆BOC)

ar(∆DCB) = ar(∆ACB)

(iii) चूँकि DCS और ACB दोनों एक ही आधार CB पर हैं और इनका क्षेत्रफल समान है।

वे एक ही समान्तर रेखाओं CB और DA के बीच स्थित हैं।

सीबी || डीए

साथ ही ∠1 = ∠2, [द्वारा (3)]

जो एकांतर आंतरिक कोण हैं।

तो, एबी || सीडी

अत: ABCD एक समांतर चतुर्भुज है।

Ex 9.3 कक्षा 9 गणित प्रश्न 7.

ABC की भुजाओं AB और AC पर क्रमशः D और E ऐसे बिंदु हैं कि ar (DBC) = ar (EBC) है। सिद्ध कीजिए कि DE || ई.पू.

समाधान:

हमारे पास ∆ABC है और बिंदु D और E इस प्रकार हैं कि ar(DBC) = ar{EBC)

चूँकि DBC और EBC एक ही आधार BC पर हैं और इनका क्षेत्रफल समान है।

cbse class 9 maths chapter 9

वे समान समानांतर DE और BC के बीच स्थित होने चाहिए।

इसलिए, DE || BC

Ex 9.3 कक्षा 9 गणित प्रश्न 8।

XY एक ABC की भुजा BC के समांतर एक रेखा है। अगर बीई ||एसी और सीएफ || AB, XY से क्रमशः E और F पर मिलता है, दर्शाइए कि ar (ABE) =ar (ACF)

समाधान:

हमारे पास एक ABC ऐसा है कि XY || ईसा पूर्व,

बीई || एसी और सीएफ || एबी.

चूंकि, XY ||BC और BE || CY

BCYE एक समांतर चतुर्भुज है।

ncert solutions for class 9 maths in hindi medium pdf

अब, समांतर चतुर्भुज BCYE और ABE एक ही आधार 8E पर और समान समांतर रेखाओं BE और AC के बीच स्थित हैं।

∴ ar(∆ABE) = 12ar(∥gmBCYE) 

फिर से, सीएफ़ || एबी [दिया गया]

XY || BC [Given]

सीएफ़ || बीएक्स और XF || BC

BCFX एक समांतर चतुर्भुज है।

अब, ACF और समांतर चतुर्भुज BCFX एक ही आधार CF पर और समान समांतर रेखाओं AB और CF के बीच स्थित हैं।

∴ar(∆ACF) = 12ar(∥gmBCFX) …(2)

साथ ही, समांतर चतुर्भुज BCFX और समांतर चतुर्भुज BCYE एक ही आधार BC पर और समान समानांतर BC और EF के बीच स्थित हैं।

∴ ar(||gm BCFX) = ar(||gm BCYE) ………(3)

(1), (2) और (3) से, हम प्राप्त करते हैं

ar(∆BE) = ar(∆ACF)

Ex 9.3 कक्षा 9 गणित प्रश्न 9।

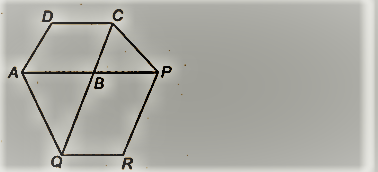
एक समांतर चतुर्भुज ABCD की भुजा AB को किसी बिंदु P तक बढ़ाया जाता है। A से होकर CP के समानांतर एक रेखा Q पर निर्मित CB से मिलती है और फिर एक समांतर चतुर्भुज PBQR पूरा होता है (आकृति देखें)।

दिखाएँ कि कुल्हाड़ी (ABCD) = ar(PBQR)।

[संकेत AC और PQ को मिलाइए। अब ar (ACQ) और ar (APQ) की तुलना करें।]

class 9 maths chapter 9 solutions pdf

समाधान:

आइए AC और PQ को मिलाएँ।

ABCD एक समांतर चतुर्भुज है [दिया है]

और AC इसका विकर्ण है, हम जानते हैं कि एक समांतर चतुर्भुज का विकर्ण इसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है।

∴ ar(∆ABC) = 12ar(∥gmABCD) …(1)

साथ ही, PBQR एक समांतर चतुर्भुज है [दिया है]

और QP इसका विकर्ण है।

∴ ar(∆BPQ) = 12ar(∥gmPBQR) …(2)

चूँकि ∆ACQ और AAPQ एक ही आधार AQ पर हैं और A के बीच समान समानांतर AQ और CP हैं।

NCERT Solutions for Class 9 Math Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.3 Q9.1

ar(∆ACQ) = ar(∆APQ)

ar(∆ACQ) – ar(∆ABQ)

= ar(∆APQ) – ar(∆ABQ)

[दोनों पक्षों से ar(∆ABQ) घटाना]

ar(∆ABC) = ar(∆BPQ) …(3)

(1), (2) और (3) से, हम प्राप्त करते हैं

12ar(∥gmABCD) = 12ar(∥gmPBQR)

 ar( ||gm ABCD) = ar(||gm PBQR)

Ex 9.3 कक्षा 9 गणित प्रश्न 10।

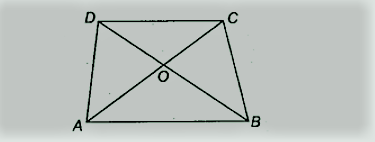
AB के साथ समलंब ABCD के विकर्ण AC और BD || DC एक दूसरे को O पर काटती है। सिद्ध कीजिए कि ar (AOD) = ar (BOC)

ncert solutions for class 9 maths in hindi medium pdf

समाधान:

BBliWWp में एक समलंब ABCD है जिसमें AB || . है CD और उसके विकर्ण AC और BD एक दूसरे को O पर काटते हैं।

चूँकि एक ही आधार पर और एक ही समान्तर रेखाओं के बीच बने त्रिभुजों के क्षेत्रफल समान होते हैं।

ABD और ABC एक ही आधार AB पर और एक ही समांतर रेखाओं AB और DC के बीच स्थित हैं

ar(∆ABD) = ar(∆ABC)

दोनों पक्षों से ar(∆AOB) घटाने पर, हम प्राप्त करते हैं

ncert solutions for class 9 maths chapter 9 प्रश्न 10

ar(∆ABD) - ar(∆AOB) = ar(∆ABC) - ar(∆AOB)

ar(∆AOD) = ar(∆BOC)

Ex 9.3 कक्षा 9 गणित प्रश्न 11.

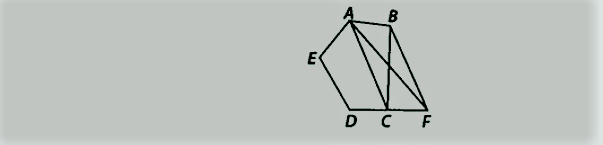
आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर एक रेखा F पर उत्पन्न DC से मिलती है। दर्शाइए कि

(i) ar (ACB) = ar (ACF)

(ii) एआर (एईडीएफ) = एआर (एबीसीडीई)

cbse class 9 maths chapter 9 exercise 9.3 solution

समाधान:

हमारे पास एक पंचभुज ABCDE है जिसमें BF || AC और DC का उत्पादन F से होता है।

(i) चूँकि समान समांतर रेखाओं और एक ही आधार पर बने त्रिभुजों का क्षेत्रफल बराबर होता है।

ACB और ACF एक ही आधार AC पर और एक ही समान्तर रेखाओं AC और BF के बीच स्थित हैं।

ar(∆ACB) = ar(∆ACF)

(ii) चूँकि, ar(∆ACB) = ar(∆ACF) [उपरोक्त सिद्ध]

दोनों पक्षों में ar(quad. AEDC) जोड़ने पर, हम प्राप्त करते हैं

⇒ ar(∆ACB) + ar(quad. AEDC) = ar(∆ACF) + ar(quad. AEDC)
∴ ar(ABCDE) = ar(AEDF)

Ex 9.3 कक्षा 9 गणित प्रश्न 12।

एक ग्रामीण इतवारी के पास चतुर्भुज के आकार का एक भूखंड है। गांव की ग्राम पंचायत ने उनके भूखंड के कुछ हिस्से को एक कोने से एक स्वास्थ्य केंद्र बनाने के लिए लेने का फैसला किया। इतवारी उपरोक्त प्रस्ताव को इस शर्त के साथ स्वीकार करता है कि उसे उसके प्लाट से लगी हुई भूमि के एवज में समान मात्रा में भूमि दी जानी चाहिए ताकि एक त्रिभुजाकार भूखण्ड बन सके। बताएं कि इस प्रस्ताव को कैसे लागू किया जाएगा।

समाधान:

हमारे पास एक चतुर्भुज ABCD के रूप में एक प्लॉट है।

आइए हम DF बनाते हैं || AC और AF और CF को मिलाइए।

class 9 maths ncert solutions

अब, DAF और DCF एक ही आधार DF पर और समान समानांतर AC ​​और DF के बीच स्थित हैं।

एआर (एडीएएफ) = एआर (एडीसीएफ)

दोनों पक्षों से ar(∆DEF) घटाने पर, हम प्राप्त करते हैं

ar(∆DAF) - ar(∆DEF) = ar(∆DCF) - ar(∆DEF)

ar(∆ADE) = ar(∆CEF)

एडीई के हिस्से को ग्राम पंचायत द्वारा अपनी (इतवारी) भूमि में भूमि (∆CEF) जोड़कर लिया जा सकता है ताकि एक त्रिकोणीय भूखंड बनाया जा सके,

यानी ABF।

आइए हम सिद्ध करें कि ar(∆ABF) = ar(quad. ABCD), हमारे पास है

एआर (एसीईएफ) = एआर (एएडीई) [उपरोक्त सिद्ध]

दोनों पक्षों में ar(quad. ABCE) जोड़ने पर, हम प्राप्त करते हैं

ar(∆CEF) + ar(quad. ABCE) = ar(∆ADE) + ar (quad. ABCE)

ar(∆ABF) = ar (quad. ABCD)

Ex 9.3 कक्षा 9 गणित प्रश्न 13.

ABCD एक समलंब है जिसमें AB || डीसी. AC के समांतर एक रेखा AB को X पर और BC को Y पर काटती है। सिद्ध कीजिए कि ar(ADX) = ar(ACY) है। [संकेत शामिल हों IX]

समाधान:

हमारे पास एक समलम्ब ABCD है जिससे AB || डीसी.

एक्सवाई || AC, AB को X पर और BC को Y पर मिलता है। आइए हम CX को मिलाएँ।

NCERT Solutions for Class 9 Maths Chapter 9 Ex 9.3 Q13

ADX और ACX एक ही आधार AX पर और एक ही समांतर रेखाओं AX और DC के बीच स्थित हैं।

ar(∆ADX) = ar(∆ACX) …(1)

ACX और ACY एक ही आधार AC पर और एक ही समान्तर रेखाओं AC और XY के बीच स्थित हैं।

ar(∆ACX) = ar(∆ACY) …(2)

(1) और (2) से, हमारे पास है

ar(∆ADX) = ar(∆ACY)

Ex 9.3 कक्षा 9 गणित प्रश्न 14.

चित्र में, , AP || BQ || CR। सिद्ध कीजिए कि ar(AQC) = ax(PBR)।

ncert solutions for class 9 maths in hindi medium pdf

समाधान:

हमारे पास है, , AP || BQ || CR

BCQ और BQR एक ही आधार BQ पर और एक ही समांतर रेखाओं BQ और CR के बीच स्थित हैं।

ar(∆BCQ) = ar(∆BQR) …(1)

ABQ और PBQ एक ही आधार BQ पर और एक ही समांतर रेखाओं AP और BQ के बीच स्थित हैं।

ar(∆ABQ) = ar(∆PBQ) …(2)

(1) और (2) को जोड़ने पर, हमारे पास है

ar(∆BCQ) + ar(∆ABQ) = ar(∆BQR) + ar(∆PBQ)

ar(∆AQC) = ar(∆PBR)

Ex 9.3 कक्षा 9 गणित प्रश्न 15।

एक चतुर्भुज ABCD के विकर्ण AC और BD 0 पर इस प्रकार प्रतिच्छेद करते हैं कि ax(AOD) = ar(BOC)। सिद्ध कीजिए कि ABCD एक समलंब है।

समाधान:

हमारे पास एक चतुर्भुज ABCD है और इसके विकर्ण AC और BD O पर इस प्रकार प्रतिच्छेद करते हैं कि

cbse class 9 maths chapter 9

ar(∆AOD) = ar(∆BOC) [दिया गया]

NCERT Solutions for Class 9 Math Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.3 Q15

दोनों पक्षों में ar(∆AOB) जोड़ने पर, हमें प्राप्त होता है

ar(∆AOD) + ar(∆AOB) = ar(∆BOC) + ar(∆AOB)

ar(∆ABD) = ar(∆ABC)

साथ ही, वे एक ही आधार AB पर हैं।

चूँकि त्रिभुज एक ही आधार पर होते हैं और उनका क्षेत्रफल समान होता है।

उन्हें एक ही समांतर रेखाओं के बीच स्थित होना चाहिए।

∴ एबी || डीसी

अब, ABCD एक चतुर्भुज है जिसमें सम्मुख भुजाओं का एक युग्म समानांतर है।

अत: ABCD एक समलंब है।

Ex 9.3 कक्षा 9 गणित प्रश्न 16।

आकृति में ax(DRC) = ar(DPC) और ai(BDP) = ar(ARC)। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब हैं।

ncert solutions for class 9 maths in hindi medium pdf

समाधान:

tfclfiftहमारे पास, ar(∆DRC) = ar(∆DPC) [दिया गया है]

और वे एक ही आधार डीसी पर हैं।

∆DRC और ∆DPC समान समांतर रेखाओं के बीच स्थित होना चाहिए।

तो, DC || RP यानि चतुर्भुज DCPR की सम्मुख भुजाओं का एक युग्म समांतर होता है।

चतुर्भुज DCPR एक समलंब है।

फिर से, हमारे पास है

ar(∆BDP) = ar(∆ARC) [दिया गया] …(1)

साथ ही, ar(∆DPC) = ar(∆DRC) [दिया गया] …(2)

(1) से (2) घटाने पर, हम प्राप्त करते हैं

ar(∆BDP) - ar(∆DPC) = ar(∆ARQ - ar(∆DRQ)

ar(∆BDC) = ar(∆ADC)

और वे एक ही आधार डीसी पर हैं।

ABDC और AADC को एक ही समान्तर रेखाओं के बीच स्थित होना चाहिए।

तो, AB || DC अर्थात चतुर्भुज ABCD की सम्मुख भुजाओं का एक युग्म समांतर है।

चतुर्भुज ABCD एक समलंब है।

ncert solutions for class 9 maths chapter 9 exercise 9.4

Ex 9.4 कक्षा 9 गणित प्रश्न 1.

समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार AB पर हैं और इनका क्षेत्रफल समान है। दिखाएँ कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से बड़ा है।

समाधान:

हमारे पास एक समांतर चतुर्भुज ABCD और आयत ABEF इस प्रकार है कि

ar(||gm ABCD) = ar(रेक्ट। ABEF)

ncert solutions for class 9 maths 

NCERT Solutions for Class 9 Maths Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.4 Q1

एबी = सीडी [समांतर चतुर्भुज के विपरीत पक्ष]

और AB = EF [एक आयत की सम्मुख भुजाएँ]

⇒ सीडी = ईएफ

एबी + सीडी = एबी + ईएफ … (1)

BE <BC और AF <AD [एक समकोण त्रिभुज में, कर्ण सबसे लंबी भुजा है] (BC + AD) > (BE + AF) …(2)

(1) और (2) से, हमारे पास है

(एबी + सीडी) + (बीसी + एडी)> (एबी + ईएफ) + बीई + एएफ)

(एबी + बीसी + सीडी + डीए)> (एबी + बीई + ईएफ + एफए)

समांतर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।

Ex 9.4 कक्षा 9 गणित प्रश्न 2.

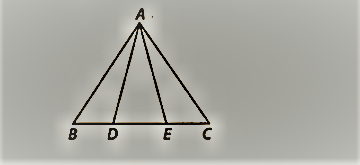
आकृति में, D और E BC पर दो बिंदु इस प्रकार हैं कि BD = DE = EC है। दिखाएँ कि ar(ABD) = ar(ADE) = ar(AEC)।

cbse class 9 maths chapter 9 solution

समाधान:

आइए हम BC पर लंब AF खींचते हैं

जैसे कि AF ABD, ADE और AEC की ऊंचाई है।

ncert solutions for class 9 maths chapter 9

Ex 9.4 कक्षा 9 गणित प्रश्न 3.

आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दिखाएँ कि ar(ADE) = ax(BCF)।

class 9 maths solutions pdf

समाधान:

चूँकि ABCD एक समांतर चतुर्भुज है [दिया है]

इसकी सम्मुख भुजाएँ समान्तर तथा समान होती हैं।

यानी, एडी = बीसी …(1)

अब, ADE और BCF बराबर आधारों पर हैं AD = BC [(1) से] और एक ही समांतर रेखाओं AB और EF के बीच।

तो, ar(∆ADE) = ar(∆BCF)।

Ex 9.4 कक्षा 9 गणित प्रश्न 4।

आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ).[संकेत AC को मिलाइए।]

class 9 maths ncert Solution

समाधान:

हमारे पास एक समांतर चतुर्भुज ABCD और AD = CQ है। आइए एसी ज्वाइन करें।

हम जानते हैं कि एक ही आधार पर और एक ही समान्तर रेखाओं के बीच बने त्रिभुजों का क्षेत्रफल बराबर होता है।

चूँकि, QAC और ∆QDC एक ही आधार QC पर और एक ही समान्तर रेखाओं AD और BQ के बीच स्थित हैं।

ar(∆QAC) = ar(∆QDC)

दोनों पक्षों से ar(∆QPC) घटाने पर, हमें प्राप्त होता है

ar(∆QAQ - ar(∆QPC) = ar(∆QDC) - ar(∆QPC)

ar(∆PAQ = ar(∆QDP) …(1)

चूँकि PAC और PBC एक ही आधार PC पर और एक ही समान्तर रेखाओं AB और CD के बीच स्थित हैं।

ar(∆PAC) = ar(∆PBC) …(2)

(1) और (2) से, हम प्राप्त करते हैं

ar(∆PBC) = ar(∆QDP)

Ex 9.4 कक्षा 9 गणित प्रश्न 5.

आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, BC का मध्य-बिंदु है। यदि AE, BC को F पर काटता है, तो दर्शाइए कि

ncert solutions for class 9 maths pdf

[संकेत EC और AD को मिलाइए। दिखाओ कि बीई || एसी और डीई || एबी, आदि]

समाधान:

आइए हम EC और AD में शामिल हों। EP ⊥ BCखींचिए।

माना AB = BC = CA = a, तो

बीडी = a/2 = डीई = बीई

ncert class 9 maths chapter 1 pdf

NCERT Solutions for Class 9 Math Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.4 Q5.1

(ii) चूँकि ABC और BED समबाहु त्रिभुज हैं।

ACB = DBE = 60°

⇒ बीई || एसी

BAE और BEC एक ही आधार BE पर और एक ही समांतर रेखाओं BE और AC के बीच स्थित हैं।

ar(∆BAE) = ar(∆BEC)

ar(∆BAE) = 2 ar(∆BDE) [DE, EBC की माध्यिका है। एआर(∆BEC) = || एआर (∆बीडीई)]

ar(ABDE) = 1/2ar(∆BAE)

(iii) ar(∆ABC) = 4 ar(∆BDE)[(i) भाग में सिद्ध]

ar(∆BEC) = 2 ar(∆BDE)

[ DE BEC की माध्यिका है]

ar(∆ABC) = 2 ar(∆BEC)

(iv) चूँकि ABC और BDE समबाहु त्रिभुज हैं।

ABC = BDE = 60°

⇒ AB || DE

BED और AED एक ही आधार ED पर और समान समांतर रेखाओं AB और DE के बीच स्थित हैं।

ar(∆BED) = ar(∆AED)

दोनों पक्षों से ar(AEFD) घटाने पर, हम प्राप्त करते हैं

ar(∆BED) – ar(∆EFD) = ar(∆AED) – ar(∆EFD)

ar(∆BEE) = ar(∆AFD)

(v) समकोण ABD में, हम प्राप्त करते हैं

NCERT Solutions for Class 9 Math Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.4 Q5.2

(1) और (2) से, हम प्राप्त करते हैं

ar(∆AFD) = 2 ar(∆EFD)

ar(∆AFD) = ar(∆BEF) [से (iv) भाग]

ar(∆BFE) = 2 ar(∆EFD)

(vi) ar(∆AFC) = ar(∆AFD) + ar(∆ADC)

= ar(∆BFE) + 1/2 ar(∆ABC) [(iv) भाग से]

= ar(∆BFE) + 1/2 x 4 x ar(∆BDE) [(i) भाग से]

= ar(∆BFE) + 2ar(∆BDE)

= 2ar(∆FED) + 2[ar(∆BFE) + ar(∆FED)]

= 2ar(∆FED) + 2[2ar(∆FED) + ar(∆FED)] [(v) भाग से]

= 2ar(∆FED) + 2[3ar(∆FED)]

= 2ar(∆FED) + 6ar(∆FED)

= 8ar (∆FED)

ar(∆FED) = 1/8 ar(∆AFC)

Ex 9.4 कक्षा 9 गणित प्रश्न 6.

एक चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि

ar(APB) x ar(CPD) = ar(APD) x ar(BPC).

[संकेत A और C से BD पर लंब खींचिए।]

समाधान:

हमारे पास एक चतुर्भुज ABCD है, जिसके विकर्ण AC और BD, P पर प्रतिच्छेद करते हैं।

आइए AM ⊥ BD और CN ⊥ BD ड्रा करें।

class 9 maths solutions pdf

Ex 9.4 कक्षा 9 गणित प्रश्न 7.

P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, AP का मध्य-बिंदु है, दर्शाइए कि

NCERT Solutions for Class 9 Maths Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Ex 9.4 Q7

समाधान:

हमारे पास एक ∆ABC इस प्रकार है कि P, AB का मध्य-बिंदु है और Q, BC का मध्य-बिंदु है।

साथ ही, R, AP का मध्य-बिंदु है। आइए हम एक्यू, आरक्यू, पीसी और पीसी से जुड़ें।

(i)  ∆APQ में, R AP का मध्य-बिंदु है। [दिया गया] B

NCERT Solutions for Class 9 Math Chapter 9 in Hindi

RQ APQ की माध्यिका है।

ar(∆PRQ) = 1/2ar(∆APQ) …(1)

ABQ में, P, AB का मध्य-बिंदु है।

QP ABQ की माध्यिका है।

ar(∆APQ) = 1/2ar(∆ABQ) …(2)

cbse class 9 maths chapter 9 exercise 9.4 solution

Ex 9.4 कक्षा 9 गणित प्रश्न 8।

आकृति में, ABC एक समकोण त्रिभुज है जो A पर समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX DE, BC से Y पर मिलता है। दर्शाइए कि

ncert solutions for class 9 maths in hindi medium pdf

(i) MBC = ABD

(ii) एआर (बीवाईएक्सडी) = 2 एआर (एमबीसी)

(iii) ar(BYXD) = ax(ABMN)

(iv)  ∆FCB ≅ ∆ACE

(v) ar(CYXE) = 2 ar(FCB)

(vi) ar(CYXE) = ax(ACFG)

(vii) ar(BCED) = ar(ABMN) + ar(ACFG)

समाधान:

हमारे पास एक समकोण ABC इस प्रकार है कि BCED, ACFG और ABMN क्रमशः इसकी भुजाओं BC, CA और AB पर वर्ग हैं। रेखा खंड AX 1 DE भी इस प्रकार खींचा गया है कि यह BC से Y पर मिलता है।

(i) ∠CBD = ∠MBA [प्रत्येक 90°]

∠CBD + ∠ABC = ∠MBA + ∠ABC

(दोनों ओर ABC जोड़ने पर)

या ∠ABD = ∠MBC

∆ABD और ∆MBC में, हमारे पास है

AB = MB [एक वर्ग की भुजाएँ]

बीडी = बीसी

∠ABD = ∠MBC [उपरोक्त सिद्ध]

∆ABD = ∆MBC [एसएएस सर्वांगसमता द्वारा]

(ii) चूँकि समांतर चतुर्भुज BYXD और ∆ABD एक ही आधार BD पर और एक ही समान्तर रेखाओं BD और AX के बीच स्थित हैं।

∴ ar(∆ABD) = 12ar(||gm BYXD)

परंतु ∆ABD ≅ ∆MBC[(i) भाग से]

चूँकि सर्वांगसम त्रिभुजों का बराबर होता है

क्षेत्र।

∴ ar(∆MBC) = 12ar(||gm BYXD)
⇒ ar(||gm BYXD) = 2ar(∆MBC)

(iii) चूंकि, ar(||gm BYXD) = 2ar(∆MBC) …(1) [(ii) भाग से]

और या(square ABMN) = 2or(∆MBC) …(2)

[एबीएमएन और एएमबीसी एक ही आधार एमबी पर हैं और एक ही समानांतर एमबी और एनसी के बीच हैं]

(1) और (2) से, हमारे पास है

ar(BYXD) = ar(ABMN) .

(iv) ∠FCA = ∠BCE (प्रत्येक 90°)

या ∠FCA+ ∠ACB = ∠BCE+ ∠ACB

[दोनों ओर ACB जोड़ने पर]

∠FCB = ∠ACE

∆FCB और ∆ACE में, हमारे पास है

FC = AC [वर्ग की भुजाएँ]

CB = CE [एक वर्ग की भुजाएँ]

∠FCB = ∠ACE [ऊपर प्रमाणित]

∆FCB ≅ ∆ACE  [एसएएस सर्वांगसमता द्वारा]

(v) चूँकि, ||gm CYXE और ∆ACE एक ही आधार CE पर और एक ही समान्तर रेखाओं CE और AX के बीच स्थित हैं।

∴ ar(||gm CYXE) = 2ar(∆ACE)

परंतु  ∆ACE ≅ ∆FCB [से (iv) भाग]

चूँकि सर्वांगसम त्रिभुज क्षेत्रफलों में बराबर होते हैं।

∴ ar (||<gm CYXE) = 2ar(∆FCB)

(vi) चूंकि, ar(||gm CYXE) = 2ar(∆FCB) …(3)

[से (v) भाग]

साथ ही (quad. ACFG) और ∆FCB एक ही आधार FC पर और समान समानांतर FC और BG के बीच स्थित हैं।

ar(quad. ACFG) = 2ar(∆FCB) …(4)

(3) और (4) से, हम प्राप्त करते हैं

ar(quad. CYXE) = ar(quad. ACFG) …(5)

(vii) हमारे पास ar(quad. BCED) है

= ar(quad. CYXE) + ar(quad. BYXD)

= ar(quad. CYXE) + ar(quad. ABMN)

[से (iii) भाग]

इस प्रकार, ar (quad. BCED)

=ar(quad. ABMN) + ar(quad. ACFG)

[से (vi) भाग]